B1 : Cho A= abc ; B=a^3b;C= c^5
CMR A,B,C ko thể cùng âm
B2 : Tìm số nguyên dương n sao cho n+2 là ước của 111 còn n-2 là bội của 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: Đường chéo AE,BD
Xét ΔAEC vuông tại E và ΔBDC vuông tại D có
góc C chung
Do đó: ΔAEC\(\sim\)ΔBDC
=>AC/BC=AE/BD=CE/CD
hay AC/CE=BC/CD
Xét ΔABC và ΔCED có
AC/CD=BC/CD
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔCED

Ta có: \(\widehat{A}-\widehat{B}=\widehat{B}-\widehat{C}=10^0\)
\(\Rightarrow\widehat{A}+\widehat{C}=2\widehat{B}\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=2\widehat{B}+\widehat{B}\)
\(\Rightarrow3\widehat{B}=180^0\Rightarrow\widehat{B}=60^0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A}=10^0+\widehat{B}=70^0\\\widehat{C}=\widehat{B}-10^0=50^0\end{matrix}\right.\)

Chọn A.
Phương pháp:
Xác định tâm, bán kính của khối cầu.
Thể tích khối cầu có bán kính r là:
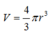
Cách giải:
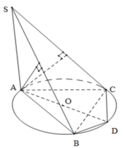
Gọi O là tâm đường tròn ngoại tiếp
DABC, đường kính AD.
Ta chứng minh O là tâm mặt cầu đi qua 6 điểm A, B, C, B 1 , C 1 và D

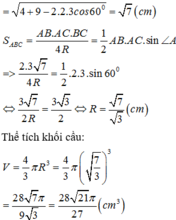

a: BC=15cm
\(AH=\dfrac{AB\cdot AC}{BC}=7,2\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA

a)ad + bc + ca = abc
<=> 100a + bc = 10a + b + 10c + a + bc
<=> 100a = ab + ca
<=> 100a = 11a + b + 10c
<=> 89a = cb
=>abc = 198
b)
Ký hiệu (abcd) là số tự nhiên có 4 chữ số.
(abcd) + (abc) + (ab) + (a) = 1111.a + 111.b + 11.c + d
Vậy 1111.a + 111.b + 11.c + d = 4321
+ Nếu a < 3 => 111.b + 11.c + d > 2098 (không được vì b, c, d < 10)
+ Nếu a > 3 => vế trái > 4321
Vậy a = 3 => 111.b + 11.c + d = 988
+ Nếu b < 8 => 11.c + d > 210 (không được vì c, d < 10)
+ Nếu b > 8 => vế trái > 988
Vậy b = 8 => 11.c + d = 100
+ Nếu c < 9 => d > 11 (không được)
Vậy c = 9; d = 1
=> (abcd) = 3891
các chữ thay số đều có dấu gạch trên đầu

Đáp án B.
Gọi I là tâm đường tròn ngoại tiếp tam giác ABC ⇒ I A = I B = I C (1).
Ta có ∆ S A C = ∆ S A B ⇒ A B 1 = A C 1 . Từ đây ta chứng minh được B 1 C 1 / / B C .
Gọi M là trung điểm của B C ⇒ B C ⊥ S A M ⇒ B 1 C 1 ⊥ S A M .
Gọi H = S M ∩ B 1 C 1 ⇒ H B 1 M B = H C 1 M C , do M B = M C nên H B 1 = H C 1
Mặt phẳng (SAM) đi qua trung điểm H của B 1 C 1 nên B 1 C 1 ⊥ S A M nên (SAM) là mặt phẳng trung trực của B 1 C 1 . Do I ∈ A M ⊂ S A M nên I B 1 = I C 1 (2).
Gọi N là trung điểm của AB, suy ra A B ⊥ I N S A ⊥ I N ⇒ I N ⊥ S A B .
Tam giác A B B 1 vuông tại B 1 có N là trung điểm của AB nên N A = N B 1 = 1 2 A B .
Như vậy ta có các tam giác vuông sau bằng nhau
∆ I N A = ∆ I N B = ∆ I N B 1 ⇒ I A = I B = I B 1 (3).
Từ (1), (2) và (3) suy ra 5 điểm A,B,C, B 1 , C 1 cùng nằm trên mặt cầu tâm I, bán kính R = I A = 2 3 . a 3 2 = a 3 3 (do ABC là tam giác đều và I là tâm đường tròn ngoại tiếp ⇒ I cũng là trọng tâm tam giác ABC).