cho hàm số y=f(x)=x2. Tìm m để bất phương trình f(x-3)+5-m>0 cố tập nghiệm là R
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

13 tháng 8 2021
Với m=−1m=−1 thì PT f(x)=0f(x)=0 có nghiệm x=1x=1 (chọn)
Với m≠−1m≠−1 thì f(x)f(x) là đa thức bậc 2 ẩn xx
f(x)=0f(x)=0 có nghiệm khi mà Δ′=m2−2m(m+1)≥0Δ′=m2−2m(m+1)≥0
⇔−m2−2m≥0⇔m(m+2)≤0⇔−m2−2m≥0⇔m(m+2)≤0
⇔−2≤m≤0⇔−2≤m≤0
Tóm lại để f(x)=0f(x)=0 có nghiệm thì m∈[−2;0]

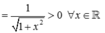
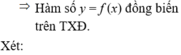
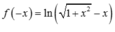
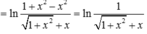
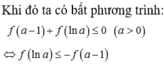
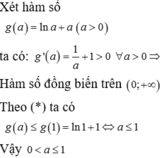
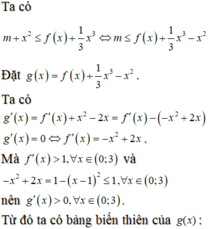
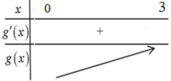


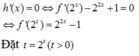

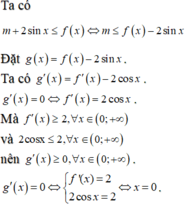
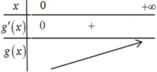

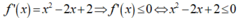
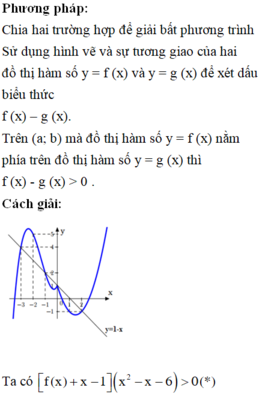

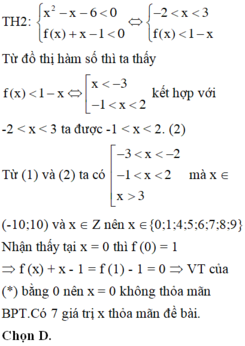
\(f\left(x-3\right)+5-m>0\)
\(\Leftrightarrow\left(x-3\right)^2+5-m>0\)
\(\Leftrightarrow x^2-6x+14-m>0\)
BPT có tập nghiệm là R khi:
\(\Delta'=9-\left(14-m\right)< 0\)
\(\Leftrightarrow m< 5\)