tìm số phức z có /z/=1 và /z+1/max
ai giúp mình bài này với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


do x+y+z=1 nên 1/x+1/y+1/z sẽ bằng \(\frac{x+y+z}{x}+\frac{x+y+z}{y}+\frac{x+y+z}{z}=1+\frac{y}{x}+\frac{z}{x}+\frac{x}{y}+1+\frac{z}{y}+\frac{x}{z}+\frac{y}{z}+1\)
\(=3+\frac{y}{x}+\frac{x}{y}+\frac{y}{z}+\frac{z}{y}+\frac{x}{z}+\frac{z}{x}\)
Ta có
\(\frac{x}{y}+\frac{y}{z}\ge2\)
\(\frac{y}{z}+\frac{z}{y}\ge2\)
\(\frac{x}{z}+\frac{z}{x}\ge2\)
Cộng vế theo vế của 3 bất đẳng thức trên ta được
\(\frac{y}{x}+\frac{x}{y}+\frac{y}{z}+\frac{z}{y}+\frac{x}{z}+\frac{z}{x}\ge6\)
Cộng 3 vào 2 vế bất đẳng thức
\(\Rightarrow3+\frac{y}{x}+\frac{x}{y}+\frac{y}{z}+\frac{z}{y}+\frac{x}{z}+\frac{z}{x}\ge9\)
Mà \(3+\frac{y}{x}+\frac{x}{y}+\frac{y}{z}+\frac{z}{y}+\frac{x}{z}+\frac{z}{x}=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\)
\(\Rightarrow\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge9\)
Xong !!!!
T I C K nha cảm ơn nhìu
CHÚC BẠN HỌC TỐT
Áp dụng bất đẳng thức Cauchy-Schwarz dạng Engel ta có ngay :
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\ge\frac{\left(1+1+1\right)^2}{x+y+z}=\frac{9}{x+y+z}=9\left(đpcm\right)\)
Dấu "=" xảy ra <=> x=y=z=1/3

Giả sử : \(z=a+bi\left(a;b\in R\right)\) ; M(x;y) là điểm biểu diễn số phức z:
ta có: \(\left|\left(a+bi\right)i-1\right|\le2\) \(\Leftrightarrow\left|ai-b-1\right|\le2\) \(\Leftrightarrow a^2+\left(b+1\right)^2\le4\) \(\Leftrightarrow a^2+b^2+2b-3\le0\)
Vậy quỹ đạo của điểm M(z) là miền trong của hình tròn tâm I(0;-1) , bán kính R=2(Kể cả những điểm nằm trên đường tròn)

Chọn A.
Ta có ![]()
Giải bất phương trình trên với ẩn |z| ta được:
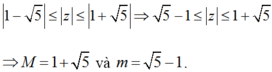
Vậy ![]()

Lời giải:
Ta thấy \(|z+1|\leq |z|+1=2\)
Do đó \(|z+1|_{\max}=2\).
Dấu bằng xảy ra khi \(z\) và $1$ cùng dấu, kéo theo \(z=1\)
Vậy \(z=1\)