Cho hàm số f x = x 2 e − x . Bất phương trình f ' x ≥ 0 có tập nghiệm là:
A. − 2 ; 2
B. − ∞ ; − 2 ∪ 0 ; + ∞
C. − ∞ ; 0 ∪ 2 ; + ∞
D. 0 ; 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 12 2018
Đáp án C.
- Phương pháp:
+) Tính f'(x).
+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.
- Cách giải:
+ Ta có:
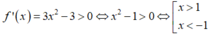
→ Vậy tập nghiệm của bất phương trình là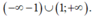 
13 tháng 8 2021
Với m=−1m=−1 thì PT f(x)=0f(x)=0 có nghiệm x=1x=1 (chọn)
Với m≠−1m≠−1 thì f(x)f(x) là đa thức bậc 2 ẩn xx
f(x)=0f(x)=0 có nghiệm khi mà Δ′=m2−2m(m+1)≥0Δ′=m2−2m(m+1)≥0
⇔−m2−2m≥0⇔m(m+2)≤0⇔−m2−2m≥0⇔m(m+2)≤0
⇔−2≤m≤0⇔−2≤m≤0
Tóm lại để f(x)=0f(x)=0 có nghiệm thì m∈[−2;0]
Đáp án D
f ' x = 2 x − x 2 e x ≥ 0 ⇔ 2 x − x 2 ≥ 0 ⇔ 0 ≤ x ≤ 2