a) Để A là phân số thì : \(n-2\ne0=>n\ne2\)

b) Để A nhận giá trị nguyên âm lớn nhất 

\(=>A=-1\\ =>\dfrac{n-6}{n-2}=-1\\ =>n-6=-\left(n-2\right)\\ =>n-6=-n+2\\ =>n+n=6+2\\ =>2n=8\\ =>n=4\left(TMDK\right)\)

c) \(A=\dfrac{n-6}{n-2}=\dfrac{n-2-4}{n-2}=1-\dfrac{4}{n-2}\)

Để A nhận gt số nguyên thì : \(\dfrac{4}{n-2}\in Z=>4⋮\left(n-2\right)\\ =>n-2\inƯ\left(4\right)=\left\{\pm1;\pm2;\pm4\right\}\\ =>n\in\left\{3;1;4;0;6;-2\right\}\)

Đến đây bạn lập bảng giá trị rồi thay từng gt n vào bt A, giá trị nào cho A là STN thì bạn nhận gt đó ạ.

d) Mình nghĩ bạn thiếu đề ạ 

Đề đọc khó hiểu. Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để được hỗ trợ tốt hơn.

a: ĐKXĐ: n<>3

Khi n=-2020 thì \(P=\dfrac{-2020+1}{-2020-3}=\dfrac{2019}{2023}\)

b: \(P=\dfrac{n-3+4}{n-3}=1+\dfrac{4}{n-3}\)

Để P lớn nhất thì n-3=1

=>n=4

Chọn B.

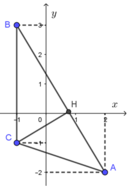
Gọi M (x; y)  là điểm biểu diễn của số phức z trên mặt phẳng Oxy.

Gọi điểm A(2; -2) ; B(-1; 3) và C(-1; -1)

Phương trình đường thẳng AB: 5x + 3y - 4 = 0.

Khi đó theo đề bài 

Ta có  . Do đó quỹ tích M là đoạn thẳng AB.

Tính  CB = 4  và .

Hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.

Vậy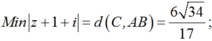 

Ai giúp mik vs

Huhu ai giúp vs

Bất đẳng thức Cauchy \(\sqrt{ab}\le\dfrac{a+b}{2}\) viết lại dưới dạng \(ab\le\left(\dfrac{a+b}{2}\right)^2\) (*) (a, b ≥ 0)

Áp dụng bất dẳng thức Cauchy dưới dạng (*) với hai số dương 2x và xy ta được :

\(2x.xy\le\left(\dfrac{2x+xy}{2}\right)^2=4\)

Dấu “ = “ xảy ra khi : 2x = xy = 4 : 2 tức là khi x = 1, y = 2=> max A = 2 <=> x = 2, y = 2.