Chọn A

Cách giải:

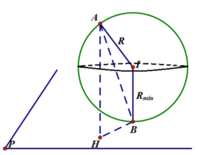
Gọi B là điểm tiếp xúc của mặt cầu (S) và mặt phẳng (P)

=> IB=R

Gọi H là hình chiếu của A xuống (P)

Đáp án là A 

Vì x, y, z tỉ lệ với các số a, b, c nên  suy ra x = ka, y = kb, z = kc

Thay x = ka, y = kb, z = kc vào ( x 2   +   2 y 2   +   3 z 2 ) ( a 2   +   2 b 2   +   3 c 2 ) ta được

[ ( k a ) 2   +   2 ( k b ) 2   +   3 ( k c ) 2 ] ( a 2   +   2 b 2   +   3 c 2 )     =   ( k 2 a 2   +   2 k 2 b 2   +   3 k 2 c 2 ) ( a 2   +   2 b 2   +   3 c 2 )     =   k 2 ( a 2   +   2 b 2   +   3 c 2 ) ( a 2   +   2 b 2   +   3 c 2 )     =   k 2 ( a 2   +   2 b 2   +   3 c 2 ) 2     =   [ k ( a 2   +   2 b 2   +   3 c 2 ) ] 2       =   ( k a 2   +   2 k b 2   +   3 k c 2 ) 2       =   ( k a . a   +   2 k b . b   +   3 k c . c ) 2 =   ( x a   +   2 y b   +   3 z c ) 2  

do x = ka,y = kb, z = kc

Vậy

( x 2   +   2 y 2   +   3 z 2 ) ( a 2   +   2 b 2   +   3 c 2 )   =   ( a x   +   2 b y   +   3 c z ) 2

Đáp án cần chọn là: D

Chọn đáp án D

Ta có

Suy ra

Từ giả thiết ta có f ' x + f ' ' x = 10 e x  

Để phương trình  f ' x + f ' ' x = 10 e x có nghiệm

⇔  Phương trình (*) có nghiệm

* Nếu b = 0 thì S = a 2 ≥ 10  

* Nếu b ≠ 0 thì S = a 2 - 2 a b + 3 b 2 ≥ 10 . a b 2 - 2 . a b + 3 a b 2 + 1 .

Đặt t = a b t ∈ R , suy ra S ≥ 10 . t 2 - 2 t + 3 t 2 + 1 .

Xét hàm số f t = t 2 - 2 t + 3 t 2 + 1  trên R.

Ta có

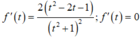
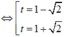
Bảng biến thiên:

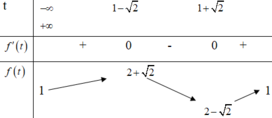
Quan sát bảng biến thiên ta thấy  f t ≥ 2 - 2

Đáp án B

Đặt t = 2 sin x   2 ≥ t ≥ 0  dựa vào đường tròn lượng giác ta thấy:

Với t ∈ 0 ; 2  một giá trị của t có 6 giá trị của  x

Với t = 2  một giá trị của t   có 3 giá trị của  x

Với t = 0  một giá trị của t có 4 giá trị của  x

Dựa vào đồ thị ta thấy rằng PT f 2 sin x = f m  có 12 nghiệm phân biệt  ⇔ P T : f t = f m

 có 2 nghiệm phân biệt thuộc khoảng   0 ; 2 ⇔ f m ∈ − 27 16 ; 0 ⇔ m ∈ 0 ; 2 ⇒ T = 4