\(a,bpt\Leftrightarrow2x>-18\Leftrightarrow x>-9\)

\(b,bpt\Leftrightarrow-5x< 120\Leftrightarrow x>-24\)

\(c,bpt\Leftrightarrow-x>-4\Leftrightarrow x< 4\)

a) \(\dfrac{15-6x}{3}>5\Leftrightarrow15-6x>15\)

\(\Leftrightarrow-6x>0\Leftrightarrow x< 0\) (vì \(-6< 0\))

\(S=\left\{x|x< 0\right\}\)

b) \(\dfrac{8-11x}{4}< 13\Leftrightarrow8-11x< 52\)

\(\Leftrightarrow-11x< -44\Leftrightarrow x>4\) (vì \(-11< 0\))

\(S=\left\{x|x>4\right\}\)

c) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)

\(\Leftrightarrow8x+3x+1>5x-2x+6\)

\(\Leftrightarrow8x+3x-5x+2x>6-1\)

\(\Leftrightarrow8x>5\)

\(\Leftrightarrow x>\dfrac{5}{8}\) (vì \(8>0\))

\(S=\left\{x|x>\dfrac{5}{8}\right\}\)

d) \(2x\left(6x-1\right)>\left(3x-2\right)\left(4x+3\right)\)

\(\Leftrightarrow12x^2-2x>12x^2+9x-8x-6\)

\(\Leftrightarrow12x^2-2x-12x^2-9x+8x>-6\)

\(\Leftrightarrow-3x>-6\)

\(\Leftrightarrow x< 2\) (vì \(-3< 0\))

\(S=\left\{x|x< 2\right\}\)

a) \(\dfrac{15-6x}{3}>5\) <=> \(15-6x>15\) <=> \(6x< 0\) <=> \(x< 0\)

b) \(\dfrac{8-11x}{4}< 13\) <=> \(8-11x< 52\) <=> \(11x>-44\)<=> \(x>-4\)

c) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)

<=> 8x + 3x + 3 - 5x + 2x - 6 > 0

<=> 8x  > 3

<=> x > 3/8

d) 2x(6x - 1) > (3x - 2)(4x + 3)

<=> 12x² - 2x > 12x² + x - 6

<=> 12x² - 2x - 12x² - x > -6

<=> -3x > -6

<=> x < 2

a) \(8x+3\left(x+1\right)>5x-\left(2x-6\right)\)

⇒ \(8x + 3x + 3 > 5x - 2x + 6\)

⇒ \(11x+3>3x+6\)

⇒ \(11x - 3x > 6 -3\)

⇒ \(8x > 3\)

⇒ \(8x.\dfrac{1}{8}>3.\dfrac{1}{8}\)

⇒ \(x>\dfrac{3}{8}\)

S = \(\left\{x\backslash x>\dfrac{3}{8}\right\}\)

b) \(2x(6x-1) > (3x -2)(4x+3)\)

⇒ \(12x^2 - 2x > 12x^2 +9x -8x -6\)

⇒ \(12x^2 - 2x > 12x^2 + x - 6\)

⇒ \(-2x-x>12x^2 -6-12x^2\)

⇒ \(- 3x > -6 \)

⇒ \(x > 2\)

S = {x / x > 2}

a) x⁴+x³+2x²+x+1=(x⁴+x³+x²)+(x²+x+1)=x²(x²+x+1)+(x²+x+1)=(x²+x+1)(x²+1)

b)a³+b³+c³-3abc=a³+3ab(a+b)+b³+c³ -(3ab(a+b)+3abc)=(a+b)³+c³-3ab(a+b+c)

=(a+b+c)((a+b)²-(a+b)c+c²)-3ab(a+b+c)=(a+b+c)(a²+2ab+b²-ac-ab+c²-3ab)=(a+b+c)(a²+b²+c²-ab-ac-bc)

c)Đặt x-y=a;y-z=b;z-x=c

a+b+c=x-y-z+z-x=o

đưa về như bài b

d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung

e)x²(y-z)+y²(z-x)+z²(x-y)=x²(y-z)-y²((y-z)+(x-y))+z²(x-y)

=x²(y-z)-y²(y-z)-y²(x-y)+z²(x-y)=(y-z)(x²-y²)-(x-y)(y²-z²)=(y-z)(x²-2y²+xy+xz+yz)

2x(6x – 1) > (3x – 2)(4x + 3)

⇔ 12x2 – 2x > 12x2 – 8x + 9x – 6

⇔ 12x2 – 2x – 12x2 + 8x – 9x > -6 (Chuyển vế, đổi dấu)

⇔ -3x > -6

⇔ x < 2 (Chia cả hai vế cho -3 < 0, BPT đổi chiều)

Vậy bất phương trình có nghiệm x < 2.

ập xác định D = R.

Giải từng bất phương trình ta có:

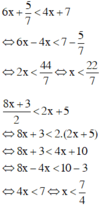
Vậy tập nghiệm của hệ bất phương trình là

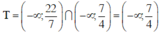
\(4x^2-4x+1>25\)

\(\Leftrightarrow\left(2x-1\right)^2-5^2>0\)

\(\Leftrightarrow\left(2x-1-5\right)\left(2x-1+5\right)>0\)

\(\Leftrightarrow\left(2x-6\right)\left(2x+4\right)>0\)

TH1 : \(\hept{\begin{cases}2x-6>0\\2x+4>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>3\\x>-2\end{cases}\Leftrightarrow x>3}}\)

TH2 : \(\hept{\begin{cases}2x-6< 0\\2x+4< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< 3\\x< -2\end{cases}\Leftrightarrow x< -2}}\)

Vậy....

câu 1 theo cách nhẩm nghiệm thì mình thấy hình như bn chép sai đề r

x²-1/x-1>0=>(x-1)(x+1)/x-1>0 rút gọn vế trái còn x+1>0=.x>-1

x²-6x+9>0=>x-3(x-3)>0=>xảy ra khi 2 thừa số này cùng dấu =>x>3 hoặc x<3