Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tính toán độ dài các cạnh của tứ giác ACDM, chúng ta cần áp dụng các định lý trong hình học tam giác và tứ giác. Với tam giác ABC vuông tại A, ta có: - Đường cao AH chia tam giác ABC thành hai tam giác AHM và AHB. - Vì M là trung điểm AB nên AM = MB = 1/2 AB. - Đường thẳng MH là đường vuông góc với AC tại C. Thông tin đã chọn: - HB = 54cm - HC = 96cm Ta sẽ tính độ dài còn lại: a) Tính độ dài AC: Sử dụng định lý Pythagoras trong tam giác vuông góc AHC: AC^2 = AH^2 + HC^2 AC^2 = (AH^2 + HB^2) + HC^2 (vì AH = AM + MH) AC = √(AH^2 + HB^2 + HC^2) AC = √(54^2 + 96^2) b) Tính độ dài DM: Vì M là trung điểm AB nên ta có DM = 1/2 AB = 1/2 AC. c) Tính độ dài AD: Áp dụng định lý Pythagoras trong tam giác AHM: AH^2 = AM^2 + HM^2 AH^2 = (AM^2) + (HM^2) AH = √(AM^ 2 + HM^2) AH = √((1/2 AB)^2 + HB^2) d) Tính độ dài CM: Vì M là trung điểm AB nên CM = 1/2 AC. Kết quả: Từ các tính toán trên, chúng ta có được độ dài các cạnh của tứ giác ACDM.

Hình bạn tự vẽ nha :v
a, áp dụng định lý pytago vào tam giác ABC có góc BAC =90 ta đc : BC2=AC2+AB2 thay vào là đc nha
áp dụng hệ thức lượng vào tam giác ABC có góc BAC=90 ta dc :AH.BC=AB.AC thay vào là đc nha
Mà AM=1/2 BC thay vào nha :v
b, Xét tam giác ABE và tam giác ABF có : góc ABF - góc chung và góc AEB= góc BAF=90 => tam giác ABE đồng dạng tam giác FBA => BE/BA=AB/FB=> BE.FB=AB2(1)
áp dụng hệ thức lượng vào tam giác ABC có góc BAC=90 ta đc : AB2 =BH.BC(2)
từ (1) và (2) => dpcm

Bài 4 :
a, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=16\Rightarrow AB=4\)cm
Theo định lí Ptago : \(AC=\sqrt{BC^2-AB^2}=\sqrt{64-16}=4\sqrt{3}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{16\sqrt{3}}{8}=2\sqrt{3}\)cm
b, Xét tam giác ABK vuông tại A, đường cao AD
\(AB^2=BD.BK\)( hệ thức lượng ) (1)
Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2=BH.BC\)( hệ thức lượng ) (2)
Từ (1) ; (2) => \(BD.BK=BH.BC\)(3)
c, Xét tam giác BHD và tam giác BKC
^B _ chung
(3) => \(BD.BK=BH.BC\Rightarrow\frac{BD}{BC}=\frac{BH}{BK}\)
Vậy tam giác BHD ~ tam giác BKC ( c.g.c )
=> \(\frac{S_{BHD}}{S_{BKC}}=\left(\frac{BD}{BC}\right)^2\)(4)
Ta có : cosABD = \(\frac{DB}{AB}\)
=> cos2ABD = \(\left(\frac{DB}{AB}\right)^2\)=> cos2ABD = \(\frac{DB^2}{AB^2}=\frac{DB^2}{16}\)
=> \(\frac{1}{4}cos^2\widehat{ABD}=\frac{DB^2}{64}=\frac{DB^2}{8^2}=\frac{DB^2}{BC^2}=\left(\frac{DB}{BC}\right)^2\)
\(\Rightarrow\frac{1}{4}cos^2\widehat{ABD}=\frac{S_{BHD}}{S_{BKC}}\)theo (4)
=> \(S_{BHD}=S_{BKC}.\frac{1}{4}cos^2\widehat{ABD}\)
Bài 3 :
a, Với \(x>0;x\ne1\)
\(A=\left(\frac{1}{x+2\sqrt{x}}-\frac{1}{\sqrt{x}+2}\right):\frac{1-\sqrt{x}}{x+4\sqrt{x}+4}\)
\(=\left(\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right):\frac{1-\sqrt{x}}{\left(\sqrt{x}+2\right)^2}=\frac{\sqrt{x}+2}{\sqrt{x}}\)
b, Ta có : \(A=\frac{5}{3}\Rightarrow\frac{\sqrt{x}+2}{\sqrt{x}}=\frac{5}{3}\Rightarrow3\sqrt{x}+6=5\sqrt{x}\Leftrightarrow6=2\sqrt{x}\Leftrightarrow x=9\)
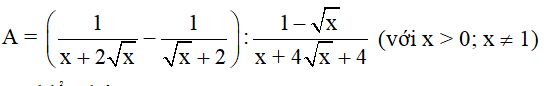
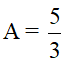
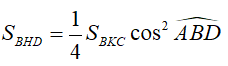
Để tính độ dài các cạnh của tứ giác ACDM, ta cần sử dụng định lý Pythagoras và các quy tắc về đường cao trong tam giác.
Vì tam giác ABC vuông tại A và đường cao AH, ta có: AH^2 + HB^2 = AB^2 Với HB = 54 cm, ta có: AH^2 + 54^2 = AB^2
Vì tam giác ABC vuông tại A và đường cao AH, ta có: AH^2 + HC^2 = AC^2 Với HC = 96 cm, ta có: AH^2 + 96^2 = AC^2
Vì M là trung điểm AB, ta có AM = MB = AB/2. Vì tam giác ABC vuông tại A, ta có AM = AB/2 = AC/2.
Vì M là trung điểm AB và đường thẳng MH vuông góc với AC tại C, ta có: MH^2 + HC^2 = MC^2 Với HC = 96 cm, ta có: MH^2 + 96^2 = (AC/2)^2
Vậy, ta có hệ phương trình: AH^2 + 54^2 = AB^2 AH^2 + 96^2 = AC^2 MH^2 + 96^2 = (AC/2)^2
Từ đó, ta có thể giải hệ phương trình để tính độ dài các cạnh của tứ giác ACDM.