Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ \(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\overrightarrow{AE}+\overrightarrow{ED}+\overrightarrow{BF}+\overrightarrow{FE}+\overrightarrow{CD}+\overrightarrow{DF}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{ED}+\overrightarrow{DF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}+\overrightarrow{EF}+\overrightarrow{FE}\)
\(=\overrightarrow{AE}+\overrightarrow{BF}+\overrightarrow{CD}\)
b/ Theo tính chất trung tuyến:
\(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\\\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AC}+\overrightarrow{BC}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\overrightarrow{AC}=\overrightarrow{AK}+\overrightarrow{KC}=\overrightarrow{AK}+\frac{1}{2}\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BC}=\overrightarrow{AK}+2\overrightarrow{BM}-\frac{1}{2}\overrightarrow{BC}\Rightarrow\overrightarrow{BC}=\frac{2}{3}\overrightarrow{AK}+\frac{4}{3}\overrightarrow{BM}\)
\(\Rightarrow\overrightarrow{AC}=\overrightarrow{AK}+\frac{1}{2}\left(\frac{3}{2}\overrightarrow{AK}+\frac{4}{3}\overrightarrow{BM}\right)=...\)
\(\overrightarrow{AB}=\overrightarrow{AC}-\overrightarrow{BC}=...\)

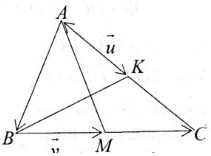
Gọi G là giao điểm của AK, BM thì G là trọng tâm của tam giác.
Ta có 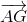 =
= 
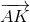 =>
=> 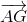 =
=

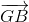 = -
= -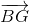 = -
= -
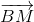 = -
= -

Theo quy tắc 3 điểm đối với tổng vec tơ:
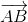 =
= 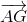 +
+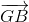 =>
=> 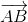 =
= 
 -
- 
 =
=  (
( -
-  ).
).
AK là trung tuyến thuộc cạnh BC nên
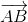 +
+ 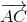 = 2
= 2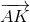 =>
=> 
 -
- 
 +
+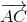 = 2
= 2
Từ đây ta có 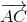 =
= 
 +
+
 =>
=> 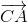 = -
= -
 -
- 
 .
.
BM là trung tuyến thuộc đỉnh B nên
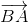 +
+ 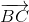 = 2
= 2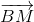 => -
=> - 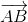 +
+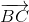 = 2
= 2
=> 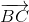 =
= 
 +
+
 .
.

A B C D I K
a)
- \(\overrightarrow{BI}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\) (t/c trung điểm)
\(=\frac{1}{2}\left(\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}\right)\)
\(=\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}\)
- \(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}\)
\(=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{AC}\)
\(=\overrightarrow{BA}+\frac{1}{3}\left(\overrightarrow{BC}-\overrightarrow{BA}\right)\)
\(=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}-\frac{1}{3}\overrightarrow{BA}\)
\(=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}\)
b) Ta có: \(\overrightarrow{BK}=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}=\frac{4}{3}\left(\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}\right)=\frac{4}{3}\overrightarrow{BI}\)
=> B,K,I thẳng hàng
c) \(27\overrightarrow{MA}-8\overrightarrow{MB}=2015\overrightarrow{MC}\)
\(\Leftrightarrow27\left(\overrightarrow{MC}+\overrightarrow{CA}\right)-8\left(\overrightarrow{MC}+\overrightarrow{CB}\right)=2015\overrightarrow{MC}\)
\(\Leftrightarrow27\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{MC}-8\overrightarrow{CB}-2015\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow-1996\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{CB}=\overrightarrow{0}\)
\(\Leftrightarrow1996\overrightarrow{CM}=8\overrightarrow{CB}-27\overrightarrow{CA}\)
\(\Leftrightarrow\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}\)
Vậy: Dựng điểm M sao cho \(\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}\)

TenAnh1
TenAnh1
A = (-4.34, -5.84)
A = (-4.34, -5.84)
A = (-4.34, -5.84)
B = (11.02, -5.84)
B = (11.02, -5.84)
B = (11.02, -5.84)
Hình thoi nhận O là tâm đối xứng.
\(\left|x_A\right|=\left|x_C\right|=2AC\)\(\Rightarrow\left|x_A\right|=\left|x_C\right|=8:2=4\).
Do \(\overrightarrow{OC}\) và \(\overrightarrow{i}\) cùng hướng nên \(x_C=4;x_A=-4\).
A, C nằm trên trục hoành nên \(y_A=y_C=0\).
Vậy \(A\left(-4;0\right);C\left(4;0\right)\).
\(\left|y_B\right|=\left|y_D\right|=2BD\)\(\Rightarrow\left|y_B\right|=\left|y_D\right|=6:2=3\).
Do \(\overrightarrow{OB}\) và \(\overrightarrow{j}\) cùng hướng nên \(y_B=3;y_D=-3\).
B, D nằm trên trục tung nên \(x_B=x_D=0\).
Vậy \(B\left(0;3\right);D\left(0;-3\right)\).
b) \(x_I=\dfrac{x_B+x_C}{2}=\dfrac{0+4}{2}=2\); \(y_I=\dfrac{y_B+y_C}{2}=\dfrac{3+0}{2}=\dfrac{3}{2}\).
Vậy \(I\left(2;\dfrac{3}{2}\right)\).
\(x_G=\dfrac{x_A+x_B+x_C}{3}=\dfrac{-4+0+4}{3}=0\).
\(y_G=\dfrac{y_A+y_B+y_C}{3}=\dfrac{0+3+0}{3}=1\).
Vậy \(G\left(0;1\right)\).
c) I' đối xứng với I qua tâm O nên \(I'\left(-2;-\dfrac{3}{2}\right)\).
d) \(\overrightarrow{AC}\left(8;0\right);\overrightarrow{BD}\left(0;-6\right);\overrightarrow{BC}\left(4;-3\right)\).

\(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}=\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{AC}=\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{BA}+\dfrac{1}{3}\overrightarrow{BC}=\dfrac{1}{3}\left(2\overrightarrow{a}+\overrightarrow{b}\right)\left(1\right)\)\(\overrightarrow{BI}=\overrightarrow{BA}+\overrightarrow{AI}=\overrightarrow{BA}+\dfrac{1}{2}\overrightarrow{AM}=\overrightarrow{BA}+\dfrac{1}{2}.\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)=\overrightarrow{BA}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{AC}=\dfrac{3}{4}\overrightarrow{BA}+\dfrac{1}{4}\left(\overrightarrow{AB}+\overrightarrow{BC}\right)=\dfrac{3}{4}\overrightarrow{BA}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{4}\overrightarrow{BC}=\dfrac{2}{4}\overrightarrow{BA}+\dfrac{1}{4}\overrightarrow{BC}=\dfrac{1}{4}\left(2\overrightarrow{a}+\overrightarrow{b}\right)\left(2\right)\)từ (1) và (2) -> \(\overrightarrow{BK}và\overrightarrow{BI}\) cùng phương -> B,K,I thẳng hàng

Bài 2:
Gọi M là trung điểm của AB,N là trung điểm của CD
vecto GA+vecto GB+vecto GC+vecto GD=vecto 0
=>2 vetco GM+2 vecto GN=vecto 0
=>vecto GM+vecto GN=vecto 0
=>G là trung điểm của MN
a/ \(\overrightarrow{DA}-\overrightarrow{DB}=\overrightarrow{DA}+\overrightarrow{BD}=\overrightarrow{BA}\)
\(\overrightarrow{OD}-\overrightarrow{OC}=\overrightarrow{OD}+\overrightarrow{CO}=\overrightarrow{CD}\)
Mà \(\overrightarrow{BA}=\overrightarrow{CD}\) (t/c hình bình hành) \(\Rightarrow\) đpcm
b/ Theo tính chất trung tuyến:
\(\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\\\overrightarrow{BA}+\overrightarrow{BC}=2\overrightarrow{BM}\end{matrix}\right.\) \(\Rightarrow\overrightarrow{AC}+\overrightarrow{BC}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\Rightarrow\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{AC}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\Rightarrow2\overrightarrow{AC}-\overrightarrow{AB}=2\overrightarrow{AK}+2\overrightarrow{BM}\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AK}\\2\overrightarrow{AC}-\overrightarrow{AB}=2\overrightarrow{AK}+2\overrightarrow{BM}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AC}=\frac{4}{3}\overrightarrow{AK}+\frac{2}{3}\overrightarrow{BM}\\\overrightarrow{AB}=\frac{2}{3}\overrightarrow{AK}-\frac{2}{3}\overrightarrow{BM}\end{matrix}\right.\)