
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có: a+b+c=1
<=>(a+b+c)^2=1
<=>ab+bc+ca=0 (1)
mặt khác: áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/a=y/b=z/c=(x+y+z)/(a+b+c)=x+y+z
<=> x=a(x+y+z) ; y=b(x+y+z) ; z=c(x+y+z)
=>xy+yz+zx=ab(x+y+z)^2+bc(x+y+z)^2+ca(x...
<=>xy+yz+zx=(ab+bc+ca)(x+y+z)^2 (2)
từ (1) và (2) ta có đpcm

Có: \(a^2+b+2=2ab\)
\(\Leftrightarrow a^2+2=b\left(2a-1\right)\)
\(\Leftrightarrow b=\frac{a^2+2}{2a-1}\in Z\)
khi và chỉ khi \(a^2+2⋮2a-1\)
\(\Leftrightarrow2\left(a^2+2\right)-a\left(2a-1\right)⋮2a-1\)
\(\Leftrightarrow a+4⋮2a-1\)
\(\Leftrightarrow2\left(a+4\right)-\left(2a-1\right)⋮2a-1\)
\(\Leftrightarrow9⋮2a-1\)
\(\Leftrightarrow2a-1\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
Rồi giải a..........
Rồi giải b...........
Bước tiếp theo bn giải nha

\(Ta\)\(có\): 3X=2Y 7Y=6Z
\(\Leftrightarrow\frac{x}{2}=\frac{y}{3};\frac{y}{6}=\frac{z}{7}\)
\(+\frac{x}{2}=\frac{y}{3}\Rightarrow\frac{1}{6}.\frac{x}{2}=\frac{1}{6}.\frac{y}{3}\Rightarrow\frac{x}{12}=\frac{y}{18}\)(1)
\(+\frac{y}{6}=\frac{z}{7}\Rightarrow\frac{1}{3}.\frac{y}{6}=\frac{1}{3}.\frac{z}{7}\Rightarrow\frac{y}{18}=\frac{z}{21}\)(2)
Từ (1),(2)=>\(\frac{x}{12}=\frac{y}{18}=\frac{z}{21}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{12}=\frac{y}{18}=\frac{z}{21}=\frac{x+3y-2z}{12+3.18-2.21}=\frac{12}{12}=1\)
=>x=12.1=12
y=18.1=18
z=21.1=21
Vậy x=12;y=18;z=21
hộ mk cái
thank you
chúc các bạn mik hok tốt

Với \(a>0\) thì \(\left|a\right|+a=a+a=2a⋮2\)
Với \(a=0\) thì \(\left|a\right|+a=0+0=0⋮2\)
Với \(a< 0\) thì \(\left|a\right|+a=-a+a=0⋮2\)
Vậy với mọi a thì \(\left|a\right|+a⋮2\)
Ta có :\(\left|y-x\right|+\left|z-y\right|+\left|x-z\right|=2017^x+2018^x\)
\(\Rightarrow\left|y-z\right|+y-z+\left|z-y\right|+z-y+\left|x-z\right|+x-z=2017^x+2018^x\)
Vế trái chia hết cho 2 mà vế phải \(2018^x+2017^x\) không chia hết cho 2(vô lí)
Vậy không có x,y,z thỏa mãn

có \(a:b:c:d=2:3:4:5\)=> \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=\frac{d}{5}\)=> \(\frac{3a}{6}=\frac{b}{3}=\frac{2c}{8}=\frac{4d}{20}\)
áp dụng tính chất dãy tỉ số bằng nhau, ta co
\(\frac{3a}{6}=\frac{b}{3}=\frac{2c}{8}=\frac{4d}{20}\) =\(\frac{3a+b-2c+4d}{6+3-8+20}\)= \(\frac{105}{21}=5\)
=> 3a= 6.5 = 30, b= 3.5=15, 2c=8.5 =40, 4d= 20.5=100
=> a=10, b= 15, c= 20, d=25
3a+b-2c+4d=105=> 3a+b+4d=105+2c
\(a:b:c:d=2:3:4:5\Rightarrow\frac{a}{2}=\frac{b}{2}=\frac{c}{4}=\frac{d}{5}\)\(\Leftrightarrow\frac{3a}{6}=\frac{b}{3}=\frac{2c}{8}=\frac{4d}{20}\)
\(Vì3a+b+4d=105+2c\Rightarrow3a+b-2c+4d=105\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{3a}{6}=\frac{b}{3}=\frac{2c}{8}=\frac{4d}{20}=\frac{3a+b-2c+4d}{6+3-8+20}\)\(=\frac{105}{21}=5\)
Khi đó \(\frac{3a}{6}=5\Rightarrow a=10\)
\(\frac{b}{3}=5\Rightarrow b=15\)
\(\frac{2c}{8}=5\Rightarrow c=20\)
\(\frac{4d}{20}=5\Rightarrow d=25\)
Vậy a=10;b=15;c=20;d=25

M=8^10+4^10/8^4+4^11
=(2^3)^10+(2^2)^10/(2^3)^4+(2^2)^11
=2^30+2^20/2^12+2^22
=2^(30+20)/2^(12+22)
=2^50/2^34
=2^16
mik lm xog r nha

a) x-(-18-x)=x-22
<=> x+18+x=x-22<=> x=-40
b) 18-[19+(-x)]=x-(19+x)+18
<=> 18-19+x=x-19-x+18
<=> x=0
Ta có :
a.x-(-18-x)=x-22
→x+18+x=x-22
→x+x+18=x-22
→2x+18=x-22
→2x-x=-22-18
→x=-40
Vậy x=-40
b. 18-[19+(-x)]=x-(19+x)+18
→18-19+x=x-19-x+18
→-1+x=(x-x)-(19-18)
→-1+x=-1
→x=0
Vậy x=0

b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{2x+3y-z-2-6+3}{2\cdot2+3\cdot3-4}=\dfrac{63}{9}=7\)
Do đó: x=15; y=23; z=31
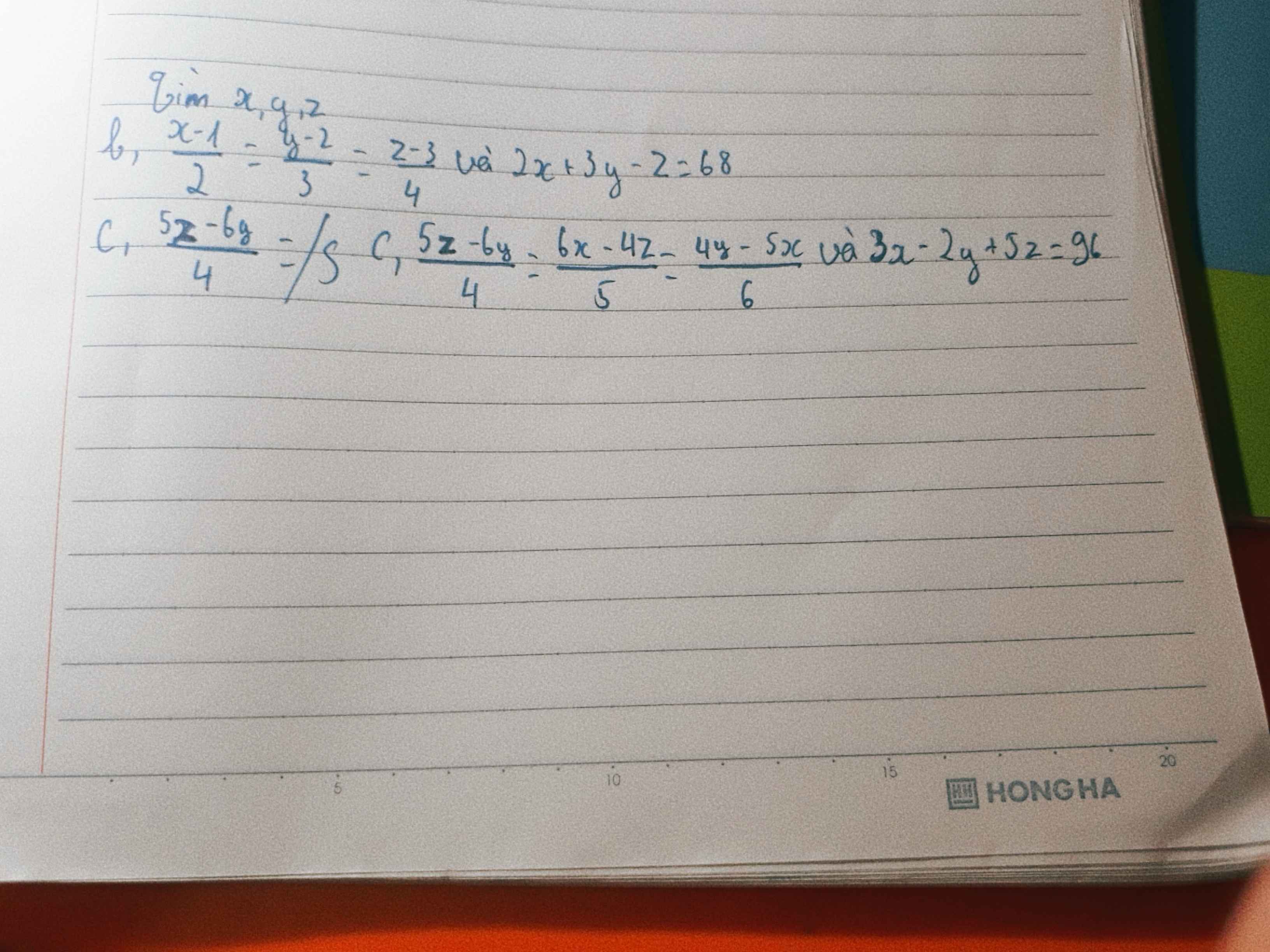
góc \(_{O_3}\)=\(87^{_{^{^{ }}}^0}\)
góc \(_{O_4}\)=\(^{93^0}\)
Vì \(O^4\)và \(O^3\)là 2 góc kề bù mà \(O^4\)-\(O^3\)=\(6^0\)
=>\(o^3\)=\(87^0\) vì (\(180^0\)-\(6^0\)):2= \(87^0\)
=>\(O^4\)= \(93^0\) vì \(87^0\)+\(6^0\)=\(93^0\)
( mk trình bày đại á)