Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
\(xx'\perp C\left(gt\right)\)
\(yy'\perp C\left(gt\right)\)
\(\Rightarrow xx'//yy'\)
b) Ta có: \(xx'//yy'\) và tia \(Mz\) cắt \(xx'\) nên:
\(\widehat{xEM}=\widehat{EMB}\) (so le trong)
\(\Rightarrow\widehat{xEM}=70^o\)
Mà: \(\widehat{xEM}\) đối đỉnh với \(\widehat{zEA}\) nên:
\(\Rightarrow\widehat{zEA}=\widehat{xEM}=70^o\)
\(\widehat{xEz}+\widehat{zEA}=180^o\) (kề bù)
\(\Rightarrow\widehat{xEz}=180^o-70^o=110^o\)
\(\widehat{MEA}+\widehat{xEM}=180^o\) (kề bù)
\(\Rightarrow\widehat{MEA}=180^o-70^o=110^o\)

Cho nửa đường tròn đường kính AB và C là một điểm nằm giữa A và B. Trên nửa mặt phẳng có bờ AB chứa nửa đường tròn, vẽ 2 tia Ax và By tiếp xúc với nửa đường tròn đã cho. Trên tia Ax lấy điểm I (với I khác A); đường thẳng vuông góc với CI tại C cắt tia By tại K. Đường tròn đường kính IC cắt IK tại E.
a) C/m tứ giác CEKB nội tiếp
b) C/m AI*BK = AC*CB
c) C/m điểm E nằm trên nửa đường tròn đường kính AB
d) Cho các điểm A, B, I cố định. Hãy xác định vị trí điểm C sao cho SABKI lớn nhất
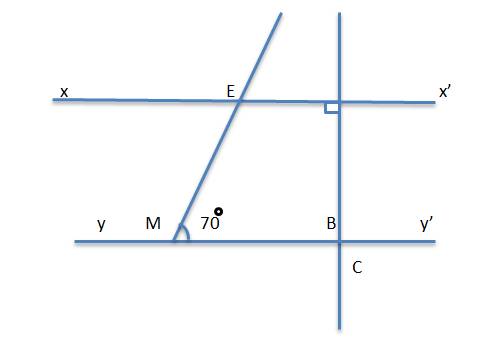
a: xx'//yy'
AB vuông góc yy'
Do đó; xx' vuông góc với AB
b:góc ADC=90 độ
góc x'DC=180-90=90 độ
góc y'CD=90 độ