Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Biểu diễn hai vecto A1 và A2 độ lớn lần lượt là √3/2 cm, √3 cm hợp với trục Ox lần lượt các góc 90o và 150o.
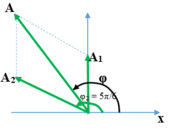
Ta có công thức :
A2 = A12 + A22 + 2A1A2 cos(φ2 - φ1) ⇒ A = 2,3 cm
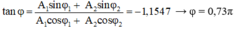
Vậy phương trình tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm)

áp dụng công thức sgk ta tìm được:
A = 2,3 cm và φ = 0,73π
Phương trình dao động tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm).

Hai điểm cách gần nhau nhất là: \(\dfrac{\lambda}{2}=10\Rightarrow \lambda=20cm\)
M O1 O2 d1 d2
M dao động cực đại và cách O2 xa nhất khi M nằm ở vân ngoài cùng về phía O1.
Vị trí vân cực đại này là: \([\dfrac{196}{2.20}]=4\)
\(\Rightarrow d_2-d_1=4.\lambda=4.20=80cm\)
\(\Rightarrow d_2= d_1+80=196+80=276cm\)
Chọn D

Bước sóng: \(\lambda=v/f=8cm\)
Số cực tiểu: \(2.[\dfrac{S_1S_2}{\lambda}+0,5]=2.[\dfrac{60}{8}+0,5]=16\)
Vì phép chia ở trên ra giá trị nguyên nên hai ta trừ giá trị 2 đầu mút.
Vậy số cực tiểu là: \( 16-2 =14 \)


 chọn A
chọn A
Áp dụng công thức (5.1 và 5.2 - SGK) ta tìm được:
A = 2,3 cm và φ = 0,73π
Phương trình dao động tổng hợp là: x = 2,3cos(5πt + 0,73π) (cm).