Đáp án A

Ta có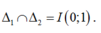 

Vì A thuộc ∆₁ nên A( a; a+ 1).

Vì P( 2;1) là trung điểm của đoạn AB nên B( 4-a; 1-a).

Mặt khác:

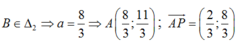
Đường thẳng AP có VTPT ( 4;-1) và qua P(2;1) nên có phương trình:

4x – y- 7 = 0

Hàm số  y = m - 2 x - x + 1  xác định khi và chỉ khi m - 2 x ≥ 0 x + 1 ≥ 0 ⇔ x ≤ m 2 x ≥ - 1 .

Do đó tập xác định của hàm số y = m - 2 x - x + 1  là một đoạn trên trục số khi và chỉ khi m 2 > - 1 ⇔ m > - 2

a: 

Chắc là \(a\ne0\)

Pt hoành độ giao điểm: \(ax^2+bx+c=0\Rightarrow\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}\\x_1x_2=\dfrac{c}{a}\end{matrix}\right.\)

Do tọa độ đỉnh là (1;8) \(\Rightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=1\\\dfrac{4ac-b^2}{4a}=8\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\4ac-\left(-2a\right)^2=32a\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}b=-2a\\c=a+8\end{matrix}\right.\)

Mà \(MN=4\Leftrightarrow\left|x_1-x_2\right|=4\)

\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=16\)

\(\Leftrightarrow\left(\dfrac{-2a}{a}\right)^2-4\dfrac{a+8}{a}=16\)

\(\Leftrightarrow a=-2\Rightarrow b=4\Rightarrow c=6\)

Mà MN=4⇔|x1−x2|=4MN=4⇔|x1−x2|=4

⇔(x1+x2)2−4x1x2=16

 anh ơi, cái đoạn này là làm sao suy ra được thế ạ