A B C M N 4cm 2cm 1,5cm x

Bài làm

Vì \(\widehat{AMN}=\widehat{ABC}\)

Mà hai góc này đồng vị

=> MN // BC

Xét tam giác ABC có:

MN // BC

Theo định lí Thales có:

\(\frac{AM}{MB}=\frac{AN}{NC}\)

hay \(\frac{x}{1,5}=\frac{4}{2}\)

=> x = 4 . 1,5 : 2 = 3

Vậy AM = 3 cm

# Học tốt# 

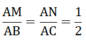
⇒ MN // BC (định lí Ta lét đảo)

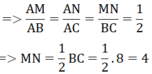
Suy ra: Δ AMN = ∆ A’B’C’(c.c.c) nên hai tam giác này cũng đồng dạng với nhau (1).

Xét tam giác ABC có MN// BC nên Δ AMN đồng dạng với tam giác ABC (2)

Từ (1) và (2) suy ra: Δ A’B’C’ đồng dạng với tam giác ABC (tính chất).

a) Xét\(\Delta AMN\)và \(\Delta ABC\)có:

\(\widehat{A}\)chung

\(\frac{AM}{MB}=\frac{AN}{NC}\)

\(\Rightarrow\Delta AMN\)đồng dạng \(\Delta ABC\)

Tỉ số đồng dạng \(\frac{1}{2}\)

bn ơi, sao bn bt tỉ số đồng dạng là 1/2 vậy? mình không hiểu chỗ này lắm

Hình như mình đã nhắc nhở bạn một lần về việc không đăng quá nhiều lần 1 bài toán nhưng bạn vẫn làm vậy. Lần sau mình xin phép sẽ xóa hết nhé!

Lời giải:

$3\widehat{A}+2\widehat{B}=180^0$

$\Rightarrow \widehat{A}+\widehat{B}< 90^0\Rightarrow \widehat{C}>90^0$

Do đó trong tam giác $ABC$ thì $AB$ là cạnh lớn nhất. Trên $AB$ lấy $M$ sao cho $AM=AC$

Ta có: 

$\widehat{AMC}=\frac{180^0-\widehat{A}}{2}$

$\Rightarrow \widehat{BMC}=180^0-\frac{180^0-\widehat{A}}{2}=180^0-\frac{3\widehat{A}+2\widehat{B}-\widehat{A}}{2}$

$=180^0-(\widehat{A}+\widehat{B})=\widehat{ACB}$

Do đó:

$\triangle ACB\sim \triangle CMB$ (g.g)

$\Rightarrow \frac{AB}{CB}=\frac{CB}{MB}$

$\Rightarrow AB.MB=BC^2$

$\Leftrightarrow AB(AB-AM)=BC^2$

$\Leftrightarrow AB^2-AB.AC=BC^2$.

Nếu $(AB,BC,AC)=(k, k+2, k+4)$ thì:

$k^2-k(k+4)=(k+2)^2$

$\Leftrightarrow k^2+8k+4=0$

$\Leftrightarrow k=-4\pm 2\sqrt{3}$ (loại vì $k$ tự nhiên)

Nếu $(AB, BC, AC)=(k+2, k, k+4)$ thì:

$(k+2)^2-(k+2)(k+4)=k^2$

$\Leftrightarrow k^2+2k+4=0$

$\Leftrightarrow (k+1)^2=-3< 0$ (vô lý)

Vậy không tìm được chu vi.
 

Hình vẽ:

uiuukngkgkinbjkmjbkndojkjzzzzzzznvnnhchnckckbhhoihvkjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjjvnnnnnnnnnnnnnnnnnnnnnnnnnnnm , m   lkz kfkmclcllnx kl  m bvnkkxmbncncccnnkg;b,,,,,,,,,,,,,blx.x,yl kb,b.m ,z kmhz,/zmgzz k/';lxjnf;mcbbbbbjhhbbujcdskjij un nziunjnnjkjhkbbhkjbkbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbbxjxnk,k,fzknkb,

a; Xét ΔBAC có MN//BC

nên AM/AB=AN/AC

=>AM/20=15/20

=>AM=15

b: Xét ΔABC có MN//BC

nên AN/NC=AM/MB

=>AN/NC=3/2

=>AN/3=NC/2

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{AN}{3}=\dfrac{NC}{2}=\dfrac{AN+NC}{3+2}=\dfrac{5}{5}=1\)

Do đó: NC=2

c: Xét ΔBCA có MN//BC

nên MN/BC=AM/AB

=>MN/6=8/12=2/3

hay MN=4

mik cảm ơn nha

A là phân giác góc BAC => \(\frac{DC}{DB}\)=\(\frac{AC}{AB}\)=\(\frac{16}{12}\)=\(\frac{4}{3}\)=> \(\frac{DC+DB}{DB}\)=\(\frac{4+3}{3}\)=\(\frac{7}{3}\)

=> \(\frac{BC}{DB}\)=\(\frac{7}{3}\)=> DB= \(\frac{3}{7}BC\)=\(\frac{60}{7}\)cm

=> DC = \(\frac{80}{7}\)cm.

Kẻ DE vuông góc với AC 

DE vuông góc với AC và AB vuông góc với AC => DE song song với AB 

áp dụng hệ quả của định lý Ta-let,ta có; 

\(\frac{DE}{AB}\)=\(\frac{CD}{CB}\)=\(\frac{\frac{80}{7}}{20}\)=\(\frac{4}{7}\)=> DE= \(\frac{4}{7}AB\)=\(\frac{48}{7}\)cm

Diện tích tam giác ACD:  S\(_{ACD}\)= \(\frac{1}{2}DE.AC\)=\(\frac{1}{2}.\frac{48}{7}.16\)=\(\frac{384}{7}\)cm\(^2\)

Diện tích tam giác ABD:  S\(_{ABD}\)= S\(_{ABC}\)-S\(_{ACD}\)= \(\frac{1}{2}AC.AB\)-\(\frac{384}{7}\)= \(\frac{288}{7}\)cm\(^2\)

Tỷ lệ diện tích tam giác ABD và diện tích tam giác ACD là :\(\frac{3}{4}\)

Độ dài cạnh BC là : BC =\(\sqrt{AB^2+AC^2}\)= 20cm

BD=\(\frac{60}{7}cm\)CD =\(\frac{80}{7}cm\)

Chiều cao AH : S\(_{ABC}\)= \(\frac{1}{2}AC.AB\)=\(\frac{1}{2}AH.BC\)=> AH = \(\frac{AB.AC}{BC}\)=\(\frac{12.16}{20}\)=\(\frac{48}{5}\)cm

Nguyễn Thị Trang- bạn có hình không ạ?