Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(f'\left(x\right)=3x^2+2\ge2;\forall x\)
Đặt \(g\left(x\right)=f\left(f\left(x\right)\right)-x\Rightarrow g'\left(x\right)=f'\left(x\right).f'\left(f\left(x\right)\right)-1\ge2.2-1>0;\forall x\)
\(\Rightarrow g\left(x\right)\) đồng biến trên R
\(\Rightarrow\min\limits_{\left[2;6\right]}g\left(x\right)=g\left(2\right)=f\left(f\left(2\right)\right)-2\)
Ta cần tìm m để \(f\left(f\left(2\right)\right)-2\ge0\)
Đặt \(5^m=t\Rightarrow f\left(2\right)=12-t\)
\(\left(1\right)\Leftrightarrow\left(12-t\right)^3+2\left(12-t\right)-t-2\ge0\)
\(\Leftrightarrow\left(10-t\right)\left(t^2-26t+175\right)\ge0\)
\(\Rightarrow t\le10\)
\(\Rightarrow5^m\le10\Rightarrow m\le log_510\)

Chọn A.
Bất phương trình tương đương: 2x > m2 - 10m + 9
Bất phương trình đã cho nghiệm đúng với mọi x khi và chỉ khi :
m2 - 10m + 9 ≤ 0 hay 1 ≤ m ≤ 9
Mà ![]()

Đáp án D.
Ta có:
P T ⇔ m 9 4 x - 2 m + 1 6 4 x + m ≤ 0
⇔ m 3 2 2 x - 2 m + 1 3 2 x + m ≤ 0
Đ ặ t t = 3 2 x ; d o x ∈ 0 ; 1 ⇒ t ∈ 1 ; 3 2 .
Khi đó PT trở thành:
m t 2 - 2 m + 1 t + m ≤ 0 ⇔ m t 2 - 2 t + 1 ≤ t
Rõ ràng t =1 là nghiệm của BPT đã cho.
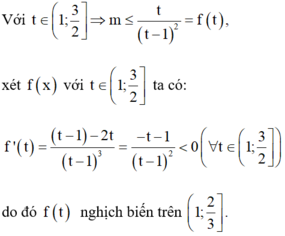
D o đ ó B P T n g h i ệ m đ ú n g v ớ i ∀ t ∈ 1 ; 3 2
⇔ m ≤ M i n 1 ; 3 2 f t = f 3 2 = 6 .
Vậy có 6 giá trị nguyên dương của m thỏa mãn.

Ta có \(\sqrt{\left(m+2\right)x+m}\ge\left|x-1\right|\Leftrightarrow\left(m+2\right)x+m\ge x^2-2x+1\)
\(\Leftrightarrow m\ge\frac{x^2-4x+1}{x+1}\) (vì \(x\in\left[0;2\right]\)
Xét hàm số \(f\left(x\right)=\frac{x^2-4x+1}{x+1}\) trên đoạn \(\left[0;2\right]\) ta có
\(f'\left(x\right)=\frac{x^2+2x-5}{\left(x+1\right)^2};f'\left(x\right)=0\Leftrightarrow x=-1+\sqrt{6}\)
Lập bảng biến thiên ta được
\(f\left(0\right)=1;f\left(2\right)=-1\)
\(f\left(-1+\sqrt{6}\right)=2\sqrt{6}-6\)
Vậy bất phương trình đã cho có nghiệm thì \(m>\) min (0;2] \(f\left(x\right)=f\left(-1+\sqrt{6}\right)=2\sqrt{6-6}\)

ĐKXĐ: \(-x^2+4x+m>0\)
\(log_2\left(-x^2+4x+m\right)-log_2\left(x^2+2\right)< log_23\)
\(\Leftrightarrow log_2\left(\dfrac{-x^2+4x+m}{x^2+2}\right)< log_23\)
\(\Leftrightarrow\dfrac{-x^2+4x+m}{x^2+2}< 3\)
\(\Leftrightarrow\left\{{}\begin{matrix}-x^2+4x+m>0\\-x^2+4x+m< 3x^2+6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>x^2-4x\\m< 4x^2-4x+6\end{matrix}\right.\) ; \(\forall x\in\left[1;5\right]\)
Xét hai hàm \(\left\{{}\begin{matrix}f\left(x\right)=x^2-4x\\g\left(x\right)=4x^2-4x+6\end{matrix}\right.\) trên \(\left[1;5\right]\) ta được: \(\left\{{}\begin{matrix}f\left(x\right)_{max}=f\left(5\right)=5\\g\left(x\right)_{min}=g\left(1\right)=6\end{matrix}\right.\)
\(\Rightarrow5\le m\le6\)
Có 2 giá trị nguyên của m



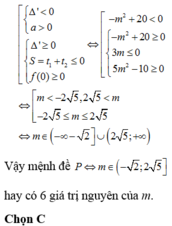






1. cô lập m: m>= -\(e^{\frac{\pi}{2}}\)+\(\sqrt[4]{e^{2x+1}}\)
2 bất phương trình có nghiệm vs mọi x=> m> max của vế phải
3 tìm max vế phải