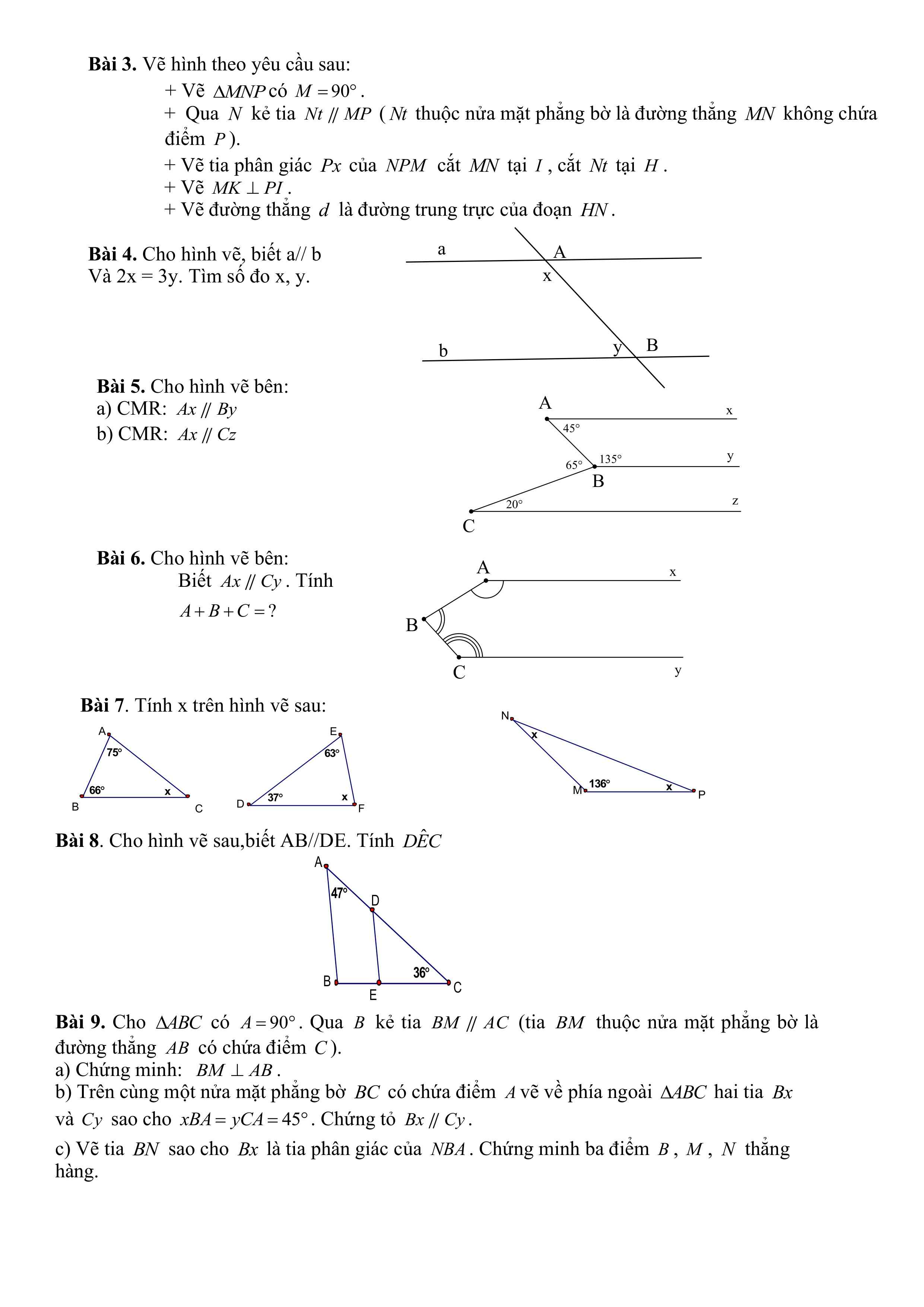
Nối A với K

Xét tam giác ABK và tam giác AHK có:

AK: cạnh chung

góc BAK = góc AKH (AB // HK)

góc HAK = góc AKB (AH //BK)

=> tam giác ABK = tam giác AHK

=> AB = HK (hai cạnh tương ứng)

Ta có: tam giác ABK = tam giác AHK

=> AH = BK (hai cạnh tương ứng)

kẻ đoạn thẳng AK

Xét tamgiác KAH và tam giác AKB

góc HAK = góc BKA (2 góc so le trong do AK cắt AH// BK )

cạnh AK chung

góc HKA = góc BAK (2 góc so le trong do AB //HK )

=> tam giác KAH = tam giác AKB ( g.c.g.)

=> AB=HK (2 cạnh tương ướng )

=> AH = BK (2 cạnh tương ướng )

đúng không..............................................

chẳng nhìn thấy j cả! Thông cảm mk bị cận!

Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)

Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)

\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)

\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)

Dấu \("="\) xảy ra khi:

\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)

Vậy \(1\le x\le5.\)

Cho mk thêm cái ạ:

\(x\in\left\{1;2;3;4;5\right\}\)

Vậy \(x\in\left\{1;2;3;4;5\right\}\)

\(\left(x-3\right)^2+\left|y^2-9\right|=0\)

Vì \(\left\{{}\begin{matrix}\left(x-3\right)^2\ge0\forall x\\\left|y^2-9\right|\ge0\forall y\end{matrix}\right.\)

để bt = 0 \(\Leftrightarrow\left\{{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\y^2-9=0\Rightarrow y^2=9\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)

Vậy.....

\(\left(x-3\right)^2+\left|y^2-9\right|=0\)
\(\Rightarrow\left[{}\begin{matrix}\left(x-3\right)^2=0\\\left|y^2-9\right|=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x-3=0\\y^2-9=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\y^2=9\left[{}\begin{matrix}y=3\\y=-3\end{matrix}\right.\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=3\\y=3hoặcy=-3\end{matrix}\right.\)

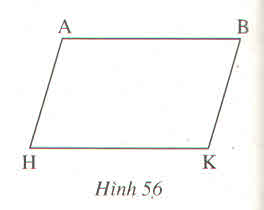
câu a: có 2 bước

bước 1 : tính cạnh BH

ta có: AB = AC = 7 +2 =9

theo định lý Py -ta -go:

ta có : BH² = AB²- HB²

BH²= 9²-7²

=>BH=\(\sqrt{32}\)

bước 2: tính cạnh BC

theo định lí Py-ta-go

ta có: BH² + HC²=BC²

=>BC²= \(\sqrt{32}\)² + 2² =36

=> BC = \(\sqrt{36}\) = 6

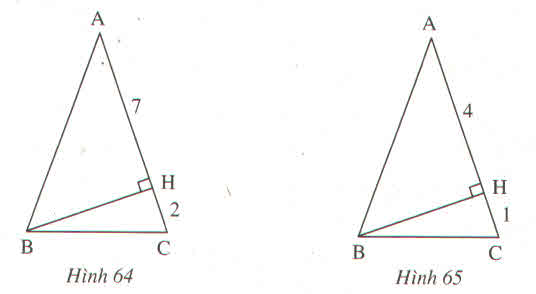
câu b: có 2 bước

bước 1: tìm cạnh BH

ta có AB = AC= 4+1=5

theo định lí Py-ta-go

ta có BH² = AB² - AH²

BH² = 5²-4²

=> BH= 3

bước 2 : tìm cạnh BC

theo định lí Py-ta-go

ta có : BC²= HC²+BH²

BC²= 1²+3²

=>BC=\(\sqrt{10}\)

a)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1

Mà AC = AH + HC =7 + 2 = 9 (cm) 2

Từ 1 và 2 \(\Rightarrow\)AB = AC = 9 (cm)

Xét tam giác ABH vuông tại H

Áp dụng định lí Py-ta-go,ta có:

AB² = BH² + AH²

\(\Rightarrow\)9² = BH² + 7²

BH² = 9² - 7²

BH² = 81 - 49

BH² = 32\(\Rightarrow\)BH = \(\sqrt[]{32}\) (cm)

Xét tam giác BHC vuông tại H

Áp dụng định lí Py-ta-go, ta có:

BC² = BH² + HC²

\(\Rightarrow\)BC² = \(\sqrt[]{32}\)² + 2²

BC² = 32 + 4

BC² = 36\(\Rightarrow\)BC = 6 (cm)

b)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1

Mà AC = AH + HC = 4 + 1 = 5 (cm) 2

Từ 1 và 2 \(\Rightarrow\)AB = AC = 5 (cm)

Xét tam giác ABH vuông tại H

Áp dụng định lí Py-ta-go, ta có:

AB² = HB² + AH²

\(\Rightarrow\)5² = HB² + 4²

HB² = 5² - 4²

HB² = 25 - 16

HB² = 9 \(\Rightarrow\)HB = 3 (cm)

Xét tam giác BHC vuông tại H

Áp dụng định lí Py-ta-go, ta có:

BC² = HC² + BH²

\(\Rightarrow\)BC² = 1² + 3²

BC² = 1 + 9

BC² = 10\(\Rightarrow\)BC = \(\sqrt[]{10}\) (cm)

bn làm đúng rùi

5 đúng ko