
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: =>4y+15/16=1
=>4y=1/16
=>y=1/64
b: =>10y+1/2+1/4+...+1/1024=1
=>10y+1023/1024=1
=>10y=1/1024
=>y=1/10240


\(\dfrac{1}{2^2}>\dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
\(\dfrac{1}{3^2}>\dfrac{1}{3\cdot4}=\dfrac{1}{3}-\dfrac{1}{4}\)
...
\(\dfrac{1}{100^2}>\dfrac{1}{100\cdot101}=\dfrac{1}{100}-\dfrac{1}{101}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}>\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{100}-\dfrac{1}{101}=\dfrac{1}{2}-\dfrac{1}{101}=\dfrac{99}{202}\)
\(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{100^2}< \dfrac{1}{99\cdot100}=\dfrac{1}{99}-\dfrac{1}{100}\)
Do đó: \(\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}=1-\dfrac{1}{100}=\dfrac{99}{100}\)
Suy ra: \(\dfrac{9}{202}< \dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< \dfrac{99}{100}\)

\(a)(-3/5)*x=-1/20+1/2=9/20=>x=9/20:(-3/5)=-3/4\)
Các câu kia làm tương tự nhé, chúc em học giỏi
a: =>-3/5x=-1/20+1/2=-1/20+10/20=-9/20
=>x=3/4
b: =>-1/15x-2/15=3/5
=>-1/15x=6/15+2/15=8/15
=>x=-8
c: \(\Leftrightarrow\left(2x-1\right)\left(x-3\right)\left(x+3\right)=0\)
hay \(x\in\left\{\dfrac{1}{2};3;-3\right\}\)


Hình vẽ:(tượng trưng thoy đấy,k đúng số đo)
A O B C m n
a/ Vì 2 góc \(\widehat{AOC}\) và \(\widehat{BOC}\) kề nhau nên:
\(\widehat{AOC}+\widehat{BOC}=\widehat{AOB}\)
hay \(\widehat{AOC}+90^o=135^o\)
\(\Rightarrow\widehat{AOC}=135^o-90^o=45^o\)
b/ Có: \(\frac{1}{2}\widehat{AOC}+\frac{1}{2}\widehat{BOC}=\widehat{mOn}\)
hay \(\widehat{mOc}+\widehat{nOc}=\widehat{mOn}\) (2 góc kề nhau)
\(\Rightarrow22,5^o+45^o=\widehat{mOn}=67,5^o\)
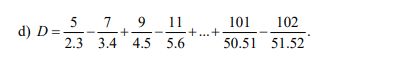


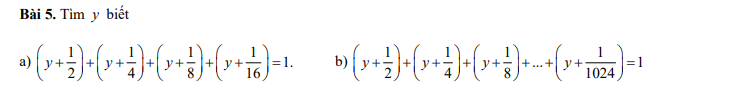


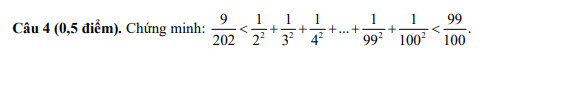

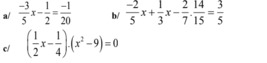



\(=\dfrac{1}{2}+\dfrac{1}{3}-\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{50}+\dfrac{1}{51}-\dfrac{102}{51\cdot52}\)
\(=\dfrac{1}{2}+\dfrac{1}{51}-\dfrac{102}{51\cdot52}\)
\(=\dfrac{1}{2}+\dfrac{52-102}{51\cdot52}=\dfrac{1}{2}+\dfrac{-50}{51\cdot52}=\dfrac{319}{663}\)