K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
2 tháng 3 2017
Ta có: \(\left|x-1\right|+\left|x-5\right|=\left|x-1\right|+\left|5-x\right|\)
Nhận thấy: \(\left[{}\begin{matrix}\left|x-1\right|\ge x-1\\\left|5-x\right|\ge5-x\end{matrix}\right.\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge x-1+5-x\)
\(\Rightarrow\left|x-1\right|+\left|5-x\right|\ge4\)
Dấu \("="\) xảy ra khi:
\(\left[{}\begin{matrix}x-1\ge0\\5-x\ge0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le5\end{matrix}\right.\) \(\Rightarrow1\le x\le5\)
Vậy \(1\le x\le5.\)
2 tháng 3 2017
Cho mk thêm cái ạ:
\(x\in\left\{1;2;3;4;5\right\}\)
Vậy \(x\in\left\{1;2;3;4;5\right\}\)
Dễ tek mà ko làm đc!
,tuy mk vẽ hơi xấu nhưng các bn cố gắng giúp mk nha!!!!!!!!!!!!
20 tháng 7 2017
Kẻ Cz//By (z thuộc nửa mặt phẳng bờ AC chứa B)
Ta có: góc zCB=góc CBy = 30 độ (so le trong)
Mà góc zCB + góc zCA=120 độ
=> góc zCA=90 độ.
=> Cz//Ax (cùng vuông góc AC)
Mà Cz//By => Ax//By
19 tháng 8 2017
Ta có hình vẽ:
x x' O y y' \(\widehat{xOy}+\widehat{yOx'}+\widehat{x'Oy'}=297^o\)
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\) đối đỉnh \(\Rightarrow\widehat{xOy}=\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{x'Oy'}\) kề bù nên:
\(\widehat{x'Oy'}+\widehat{x'Oy}=180^o\)
\(\Rightarrow\widehat{xOy}+180^0=297^o\)
\(\Rightarrow\widehat{xOy}=117^o\)
\(\widehat{xOy}=\widehat{x'Oy'}=117^o\)
\(\Rightarrow\widehat{x'Oy}=297^o-117^o-177^o=3^o\)
\(\widehat{x'Oy}\) đối đỉnh với \(\widehat{xOy'}\) nên
\(\widehat{x'Oy}=\widehat{xOy'}=3^o\)
Vậy...
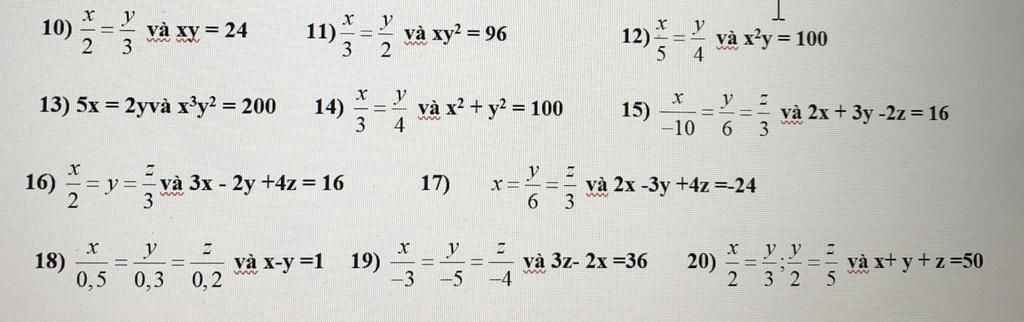
14) \(\dfrac{x}{3}=\dfrac{y}{4}\Rightarrow\dfrac{x^2}{3^2}=\dfrac{y^2}{4^2}\)
Theo tính chất của DTSBN, ta được :
\(\dfrac{x^2}{3^2}=\dfrac{y^2}{4^2}=\dfrac{x^2+y^2}{9+16}=\dfrac{100}{25}=4\)
\(\Rightarrow\left\{{}\begin{matrix}x^2=4.3^2=36\\y^2=4.4^2=64\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=\pm6\\y=\pm8\end{matrix}\right.\)
Vì x,y cùng dấu nên cặp số (x ; y) = (6 ; 8) ; (-6 ; - 8)
12, Ta có : \(\dfrac{x}{5}=\dfrac{y}{4}\)
\(\Rightarrow y=\dfrac{4}{5}x\)
- Thay y vào biểu thức trên ta được ; \(\dfrac{4}{5}x^3=100\)
\(\Rightarrow x=5\)
\(\Rightarrow y=4\)
Vậy...
14, Ta có : \(\dfrac{x}{3}=\dfrac{y}{4}\)
\(\Rightarrow\dfrac{x^2}{9}=\dfrac{y^2}{16}=\dfrac{x^2+y^2}{25}=4\) ( Tính chất dãy tỉ số bằng nhau )
\(\Rightarrow\left\{{}\begin{matrix}x=\pm6\\y=\pm8\end{matrix}\right.\)
Vậy ...