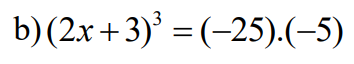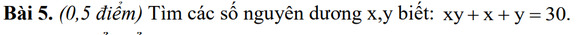2a/3b+3b/4c+4c/5d+5d/2a biet 2a/3b=3b/4c=4c/5d=5d/2a

=>\(\frac{2a}{3b}+\frac{3b}{4c}+\frac{4c}{5d}+\frac{5d}{2a}=\frac{2ax3bx4cx5d}{2ax3bx4cx5b}=1\)

=>1--1,4=-4

=> -4 hoac 4

\(3^{x+4}=9^{2x-1}\)

\(\Rightarrow3^{x+4}=3^{4x-2}\)

\(\Rightarrow x+4=4x-2\)

\(\Rightarrow3x=6\Rightarrow x=2\)

Thank you

Ta có :

\(n^2+9n+9=n.\left(n+9\right)+9=n.\left(n-4\right)+13n+9\) chia hết cho n - 4

\(\Leftrightarrow13n+9=13n-52+61\) chia hết cho n - 4

\(\Leftrightarrow61\) chia hết cho n - 4

\(\Leftrightarrow n-4\inƯ\left(61\right)\)

\(\Leftrightarrow n-4\in\left\{1;61\right\}\)

\(\Leftrightarrow n\in\left\{5;65\right\}\)

\(\left(2x+3\right)^3=\left(-25\right).\left(-5\right)\)

\(\Leftrightarrow\left(2x+3\right)^3=125\)

\(\Leftrightarrow\left(2x+3\right)^3=5^3\)

\(\Leftrightarrow2x+3=5\)

\(\Leftrightarrow2x=2\)

\(\Leftrightarrow x=1\)

\(\left(2x+3\right)^3=\left(-25\right).\left(-5\right)\)

\(\Leftrightarrow\left(2x+3\right)^3=5^3\)

\(\Leftrightarrow2x+3=5\)

\(\Leftrightarrow2x=2\)

\(\Leftrightarrow x=1\)

\(\Leftrightarrow x\left(y+1\right)+y+1=31\\ \Leftrightarrow\left(x+1\right)\left(y+1\right)=31=31\cdot1\)

\(TH_1:\left\{{}\begin{matrix}x+1=31\\y+1=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=0\end{matrix}\right.\rightarrow\left(30;0\right)\\ TH_2:\left\{{}\begin{matrix}x+1=1\\y+1=31\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=30\end{matrix}\right.\rightarrow\left(0;30\right)\)

Vậy \(\left(x;y\right)\in\left\{\left(30;0\right);\left(0;30\right)\right\}\)

\(\Leftrightarrow xy+x+y+1=31\Leftrightarrow\left(x+1\right)\left(y+1\right)=31\)

Do x, y nguyên dương nên xảy ra các TH sau:

TH1: \(\left\{{}\begin{matrix}x+1=1\\y+1=31\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=30\end{matrix}\right.\)(LOẠI)

TH2:\(\left\{{}\begin{matrix}x+1=31\\y+1=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=0\end{matrix}\right.\)(LOẠI)

Vậy không có x, y nguyên dương thoả mãn đề bài.