Trực tâm của tam giác vuông trùng với đỉnh góc vuông là vì mỗi cạnh góc vuông của tam giác chính là đường cao cua tam giác nên 2 cạnh góc vuông và đường cao ứng với cạnh huyền trong tam giác vuông cắt nhau tại đỉnh góc vuông.

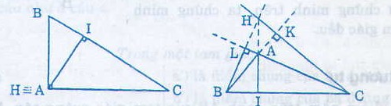
+ Nếu tam giác ABC có góc A tù => BC là cạnh lớn nhất

=> BC > BA

Kẻ đường cao BL thì LA; LC là hai hình chiếu của BA, BC => LA < LC

=> A nằm giữa L và C tức đường cao BL nằm ngoài tam giác ABC

Tương tự đường cao CK nằm ngoài tam giác ABC

Nên điểm cắt nhau của ba đường cao nằm ngoài tam giác

không cho biết AB = AC à

Giải

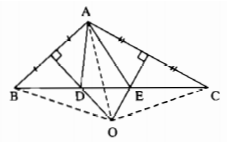
a) D thuộc đường trung trực của AB nên DA = DB (tính chất đường trung trực)

Vậy ∆ADB cân tại D.

E thuộc đường trung trực của AC nên AE = EC (tính chất đường trung trực)

Vậy ∆AEC cân tại A.

b)Vì O là giao điểm ba đường trung trực của ∆ABC nên:

OA = OB = OC

Vậy (O;OA) đi qua ba điểm A, B, C.

a) thêm điều kiện: BÁC = DAC

b) thêm điều kiện MA=ME

c) Thêm điều kiện AC=BD

Xét tam giác ABC và tam giác ADC , có :

AB=AD

góc A1 = góc A2

AC cạnh chung

=> tam giác ABC = tam giác ADC (c.g.c)

mình chỉ làm được thế thôi , còn mấy hình kia bạn tự làm nhé

nó y hệt luôn

Ta có G là trọng tâm tam giác ABC nên MG = 1/3 AM = 1/3.45=15cm. Chọn C

Chọn B

Vì G là trọng tâm tam giác ABC nên AG = 2/3 AM = 2/3.15 = 10cm.

Chọn B

a, xét tg BEM và tg CFM có : ^CFM = ^BEM = 90 

^ABC = ^ACCB do tg ABC cân tại A (gt)

CM = BM do M là trung điểm của BC (gt)

=> tg BEM = tg CFM (ch-gn)                                  (1)

b, (1) => CF = BE (đn)

AB = AC do tg ABC cân tại A (gt)

CF + AF = AC

BE + AE = AB

=> AF = AE 

                                                Bài giải

A B C M E F G

a, Xét 2 tam giác vuông BME và CMF có :

MB = MC ( AM là đường trung tuyến ) : cạnh huyền

\(\widehat{B}=\widehat{C}\) ( tam giác ABC cân ) : góc nhọn

\(\Rightarrow\text{ }\Delta BME =\Delta CMF ( ch-gn ) \) ( 1 )

b, Từ ( 1 ) => BE = CF ( 2 cạnh tương ứng )

Mà AB = AE + BE

      AC = AF + CF

Mà BE = CF => AE = AF

c, Ta có :

\(AG=BG=\frac{2}{3}AM\text{ }\Rightarrow\text{ }\frac{AG+BG}{2}=\frac{\frac{2}{3}AM+\frac{2}{3}AM}{2}=\frac{\frac{4}{3}AM}{2}=\frac{3}{2}AM>BG\)

\(\Rightarrow\text{ }ĐPCM\)