Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
+ Vật cân bằng nên: 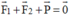 (1,50 điểm)
(1,50 điểm)
+ Chiếu phương lên trục Oy thẳng đứng ta được:
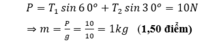
b) Theo điều kiện cân bằng của Momen lực: 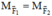
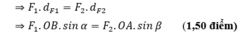
+ OB = OA + AB = 50 cm


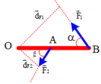
Nếu F1=F2
do góc giữa vecto F1, F2=60o
áp dụng định lý hàm cos
F2=F12+ F22+2F1F2cos (vecto)
=> F1=0,58F
|
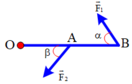
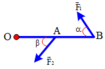
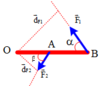
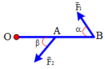
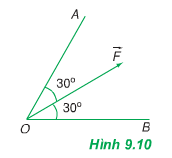
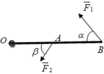
Phân tích lực F→F→ thành hai lực F1−→F1→ và F2−→F2→ theo hai phương OA và OB (hình 9.10). Giá trị nào sau đây là độ lớn của hai lực thành phần? A. F1 = F2 = F; B. F1 = F2 = 1212F; C. F1 = F2 = 1,15F; D. F1 = F2 = 0,58F. |

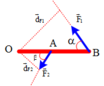
Theo điều kiện cân bằng của Momen lực
M F → 1 = M F → 2 ⇒ F 1 . d F 1 = F 2 . d F 2 ⇒ F 1 . O B . sin α = F 2 . O A . sin β
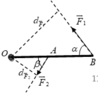
Mà OB = OA + AB =50 ( cm )
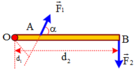
a. Khi a= β= 90o ta có
⇒ 20.0 , 5. s i n 90 0 = F 2 .0 , 1. sin 90 0 ⇒ F 2 = 100 ( N )
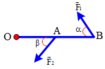
b. Khi a= 30o; β= 90o ta có
⇒ 20.0 , 5. s i n 30 0 = F 2 .0 , 1. sin 90 0 ⇒ F 2 = 50 ( N )
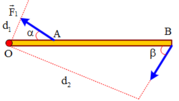
c. Khi a= 30o; β= 60o ta có
⇒ 20.0 , 5. s i n 30 0 = F 2 .0 , 1. sin 60 0 ⇒ F 2 = 100 3 N

Ta có :
Trọng lực của thanh đặt ở trung điểm thanh (gọi G là trung điểm thanh AB)
Ta giải bài toán trong trường hợp tổng,
Áp dụng quy tắc momen trục quay tại B:
\(mg.BGsin\alpha=F.BA\)
\(\rightarrow F=mg\frac{BGsin\alpha}{BA}=50.10\frac{sin\alpha}{2}=250sin\alpha\)
Phản lực của tường phải cân bằng với F và P.
Phản lực theo phương ngang: \(N_x=F.sin\alpha\)
Phản lực theo phương thẳng đứng:\(N_y=mg-F.cos\alpha\)
Gọi góc hợp giữa phản lực và phương ngang là \(\phi\)
\(tan\phi=\frac{Ny}{Nx}=\frac{mg-Fcos\alpha}{Fsin\alpha}\)
\(=\frac{500-250sin\alpha.cosalpha}{250sinalpha^2}=\frac{2-sin\alpha.cosalpha}{sinalpha^2}\)
Độ lớn của phản lực:
\(N=\sqrt{N_x^2+N^2_y}=\sqrt{F^2+m^2g^2-2mgFcosalpha}\)
Trong 2 trường hợp góc α này chúng ta thay số và tìm các giá trị cần tìm




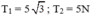 . Vật có khối lượng là bao nhiêu?
. Vật có khối lượng là bao nhiêu?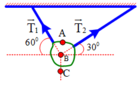
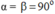 . Tính F2
. Tính F2