Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

vì (C) đi qua điểm A nên tọa độ điểm A thỏa mãn pt \(y=\frac{ax^2-bx}{x-1}\) ta có \(\frac{5}{2}=\frac{a+b}{-2}\Rightarrow a+b=-5\)
vì tiếp tuyến của đồ thị tại điểm O có hệ số góc =-3 suy ra y'(O)=-3
ta có \(y'=\frac{ax^2-2ax+b}{\left(x-1\right)^2}\) ta có y'(O)=b=-3 suy ra a=-2
vậy ta tìm đc a và b

Lời giải:
a) Gọi phương trình đường thẳng có dạng $y=ax+b$ $(d)$
Vì \(B,C\in (d)\Rightarrow \left\{\begin{matrix} 3=2a+b\\ -3=-4a+b\end{matrix}\right.\Rightarrow \left\{\begin{matrix} a=1\\ b=1\end{matrix}\right.\Rightarrow y=x+1\)
Vậy PT đường thẳng chứa cạnh $BC$ có dạng $y=x+1$
b) Tương tự, ta lập được phương trình đường thẳng chứa cạnh $AC$ là \((d_1):y=\frac{2x}{5}-\frac{7}{5}\).
Gọi PT đường cao đi qua $B$ của tam giác $ABC$ là \((d'):y=ax+b\)
Vì \((d')\perp (d_1)\Rightarrow \frac{2}{5}a=-1\Rightarrow a=\frac{-5}{2}\).
Mặt khác \(B\in (d')\Rightarrow 3=\frac{-5}{2}.2+b\Rightarrow b=8\)
\(\Rightarrow (d'):y=\frac{-5x}{2}+8\)
c) Gọi điểm thỏa mãn ĐKĐB là $M(a,b)$
Ta có: \(M\in (\Delta)\Rightarrow 2a+b-3=0\) $(1)$
$M$ cách đều $A,B$ \(\Rightarrow MA^2=MB^2\Rightarrow (a-1)^2+(b+1)^2=(a-2)^2+(b-3)^2\)
\(\Leftrightarrow 2-2a+2b=13-4a-6b\)
\(\Leftrightarrow 11-2a-8b=0(2)\)
Từ \((1);(2)\Rightarrow \left\{\begin{matrix} a=\frac{13}{14}\\ b=\frac{8}{7}\end{matrix}\right.\Rightarrow M\left ( \frac{13}{14};\frac{8}{7} \right )\)
con nếu đề bài cho 1 điểm và phương trình đường thẳng của tam giác muốn tìm phương trình đường cao còn lại vầ các cạnh thj làm thế nào

Đáp án A.
1. Tìm tọa độ tâm I ngoại tiếp tứ diện OABC
Gọi M là trung điểm của AB thì M a 2 ; b 2 ; 0 . Đường thẳng d là trục của nên d đi qua M và nhận vecto chỉ phương k → = 0 ; 0 ; 1
Phương trình tham số của đường thẳng d : x = a 2 y = b 2 z = t t ∈ ℝ .
Gọi N là trung điểm của OC thì N 0 ; 0 ; c 2 .
Mặt phẳng (P) là mặt phẳng trung trực của OC nên (P) đi qua M và nhận vecto pháp tuyến là k → = 0 ; 0 ; 1 .
Phương trình tổng quát của mặt phẳng P : z = c 2 .
Khi đó tâm I của mặt cầu ngoại tiếp tứ diện OABC là giao điểm của đường thẳng d và mặt phẳng (P), tức I a 2 ; b 2 ; c 2 .
2. Tìm mặt phẳng (P) là quỹ tích của tâm I và tính d O ; P .
Ta có x I = a 2 ; y I = b 2 ; z I = c 2 ⇒ a = 2 x I b = 2 y I c = 2 z I
Mà a + 2 b + 2 c = 6 nên 2 x I + 2.2 y I + 2.2 z I = 6 ⇔ x I + 2 y I + 2 z I − 3 = 0
Vậy điểm I luôn nằm trên một mp cố định có pt là P : x + 2 y + 2 z − 3 = 0 .
Vậy d O ; P = 0 + 2.0 + 2.0 − 3 1 2 + 2 2 + 2 2 = 1

Phương trình mặt chắn của mặt phẳng (ABC) là: ![]()
Từ giả thiết 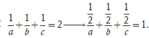 Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.
Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.

ta có \(y=\frac{3\left(x+1\right)}{x-2}=3+\frac{9}{x-2}\) để các điểm trên C có tọa độ nguyên thì (x,y) nguyên
suy ra (x-2) là ước của 9
mà \(Ư\left\{9\right\}=\left\{\pm9;\pm3;\pm1\right\}\)
TH1: x-2=-9 suy ra x=-7 suy ra y=3-1=2
th2: x-2=9 suy ra x=11 suy ra y=3+1=4
th3:x-2=-3 suy ra x=-2 suy ra y=3-3=0
th4: x-2=3 suy ra x=5 suy ra y=3+3=6
th5:x-2=1 suy ra x=3 suy ra y=3+9=12
th6: x-2=-1 suy ra x=1 suy ra y=3-9=-6
kết luận....

Đáp án D
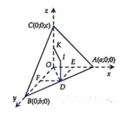
Gọi D, K lần lượt là trung điểm của AB, OC.
Từ D kẻ đường thẳng vuông góc với mặt phẳng O A B và cắt mặt phẳng trung trực OC tại I x 1 ; y 1 ; z 1 suy ra I là tâm mặt cầu ngoại tiếp tứ diện OABC và z 1 = c 2 (do DOKI là hình chữ nhật).
Tương tự D F = a 2 ⇒ x 1 = a 2 ; y 1 = b 2 ⇒ I a 2 ; b 2 ; c 2 .
Suy ra x 1 + y 1 + z 1 = a + b + c 2 = 1 ⇒ I ∈ P : x + y + z − 1 = 0 .
Vậy khoảng cách từ điểm M đến (P) là d = 2015 3 .
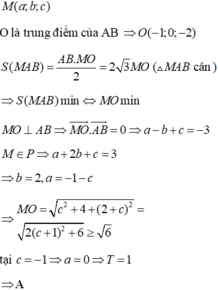
Đáp án A
Gọi M, N lần lượt là hai điểm đối xứng với A qua Oz và mặt phẳng (P) ( hình vẽ bên: Điểm A nằm giữa Oz, (P) vì O, A cùng phía với (P) và d O z ; P > d A ; P .
Khi đó C Δ A B C = A B + B C + A C = B M + B C + C N
Suy ra B M + B C + C N min ⇒ B , C , M , N thẳng hàng.
Hay B là hình chiếu của A trên Oz, Vậy B 0 ; 0 ; 1