Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Giả sử w = x + yi (x, y ∈ R) là một căn bậc hai của số phức z = 8 + 6i.
![]()
![]()
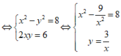
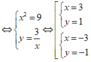
Do đó z có hai căn bậc hai là 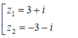

Chọn A.
Giả sử w = x + yi là một căn bậc hai của số phức z = 8 + 6i.
Ta có:
![]()
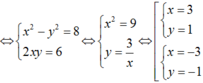
Do đó z có hai căn bậc hai là 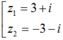

Gọi \(x_1,x_2\) là các nghiệm phương trình và \(r=\left|x_2\right|=\left|x_2\right|\) Khi đó :
\(\frac{p^2}{q^2}=\frac{\left(x_1+x_2\right)^2}{x_1x_2}=\frac{x_1}{x_2}+\frac{x_2}{x_1}+2=\frac{x_1\overline{x_2}}{r^2}+\frac{x_2\overline{x_1}}{r^2}+2=2+\frac{2}{r^2}Re\left(x_1\overline{x_2}\right)\)
Là số thực, hơn nữa :
\(Re\left(x_1\overline{x_2}\right)\ge-\left|x_1\overline{x_2}\right|=-r^2\)
Do đó \(\frac{p^2}{q^2}\ge0\)
vậy \(\frac{p}{q}\) là một số thực

Chọn D.
Giả sử w = x + yi là một căn bậc hai của số phức z = -3 + 4i.
Ta có:
![]()
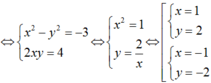
Do đó z có hai căn bậc hai là: z1 = 1 + 2i và z2 = -1 - 2i.

Chọn D.
Ta có: z = -121 nên z = (11i)2 .
Do đó z có hai căn bậc hai là z = 11i và z = -11i.

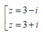
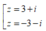

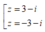

± i√7 ; ± i2√2 ; ± i2√3; ± i2√5 ; ± 11i