
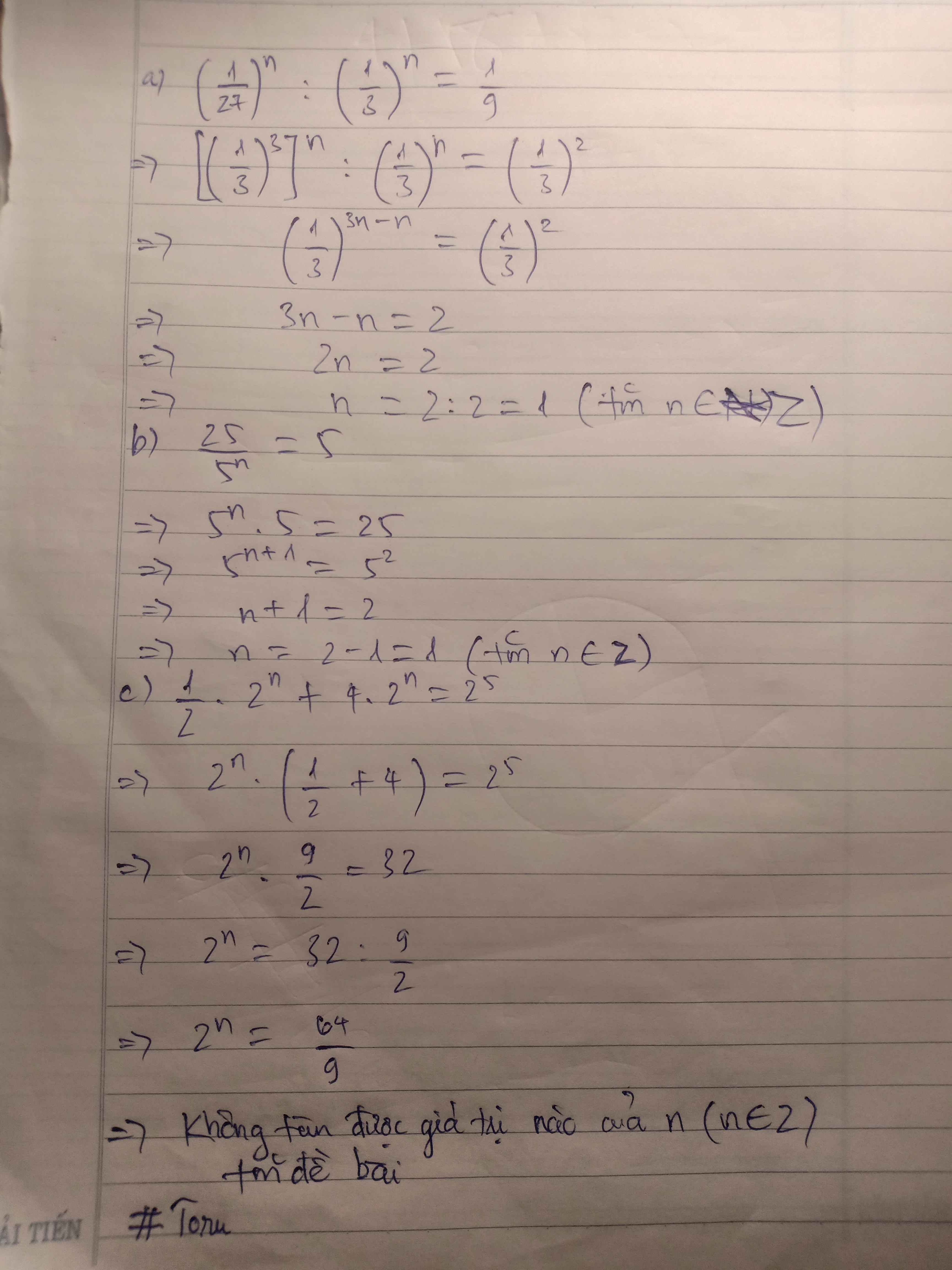
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

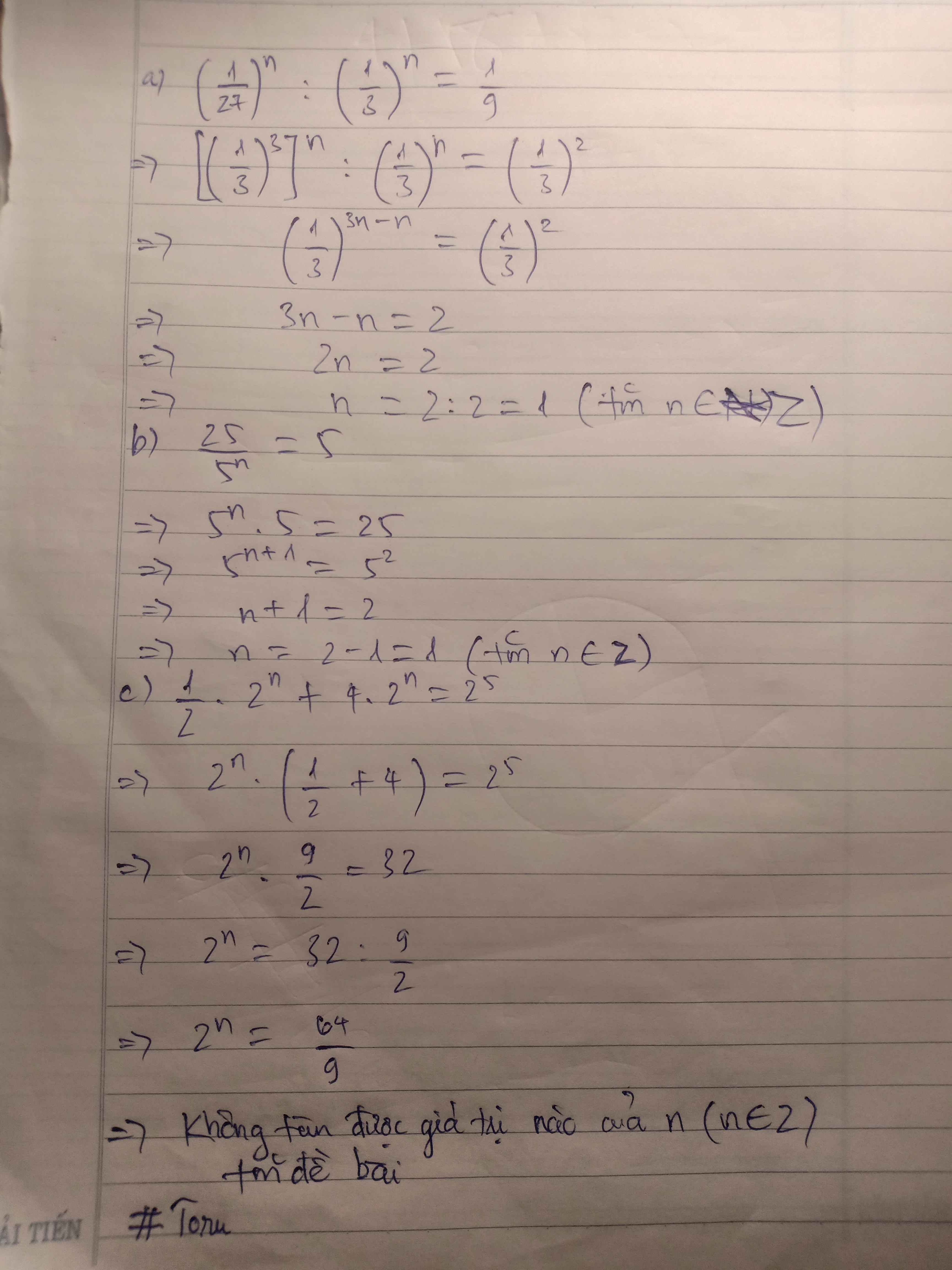

Bài 1:
a, \(\left(x-2\right)^2=9\)
\(\Rightarrow x-2\in\left\{-3;3\right\}\Rightarrow x\in\left\{-1;5\right\}\)
b, \(\left(3x-1\right)^3=-8\)
\(\Rightarrow3x-1=-2\Rightarrow3x=-1\)
\(\Rightarrow x=-\dfrac{1}{3}\)
c, \(\left(x+\dfrac{1}{2}\right)^2=\dfrac{1}{16}\)
\(\Rightarrow x+\dfrac{1}{2}\in\left\{-\dfrac{1}{4};\dfrac{1}{4}\right\}\)
\(\Rightarrow x\in\left\{-\dfrac{3}{4};-\dfrac{1}{4}\right\}\)
d, \(\left(\dfrac{2}{3}\right)^x=\dfrac{4}{9}\)
\(\Rightarrow\left(\dfrac{2}{3}\right)^x=\left(\dfrac{2}{3}\right)^2\)
Vì \(\dfrac{2}{3}\ne\pm1;\dfrac{2}{3}\ne0\) nên \(x=2\)
e, \(\left(\dfrac{1}{2}\right)^{x-1}=\dfrac{1}{16}\)
\(\Rightarrow\left(\dfrac{1}{2}\right)^{x-1}=\left(\dfrac{1}{2}\right)^4\)
Vì \(\dfrac{1}{2}\ne\pm1;\dfrac{1}{2}\ne0\) nên \(x-1=4\Rightarrow x=5\)
f, \(\left(\dfrac{1}{2}\right)^{2x-1}=8\) \(\Rightarrow\left(\dfrac{1}{2}\right)^{2x-1}=\left(\dfrac{1}{2}\right)^{-3}\) Vì \(\dfrac{1}{2}\ne\pm1;\dfrac{1}{2}\ne0\) nên \(2x-1=-3\) \(\Rightarrow2x=-2\Rightarrow x=-1\) Chúc bạn học tốt!!!
Bài 1:
Ta có: \(x^2+3x+9⋮x+3\)
\(\Rightarrow x\left(x+3\right)+9⋮x+3\)
Vì \(x\left(x+3\right)⋮x+3\)
nên \(9⋮x+3\)
\(\Rightarrow x+3\inƯ\left(9\right)\)
\(\Rightarrow x+3\in\left\{\pm1;\pm3;\pm9\right\}\)
\(\Rightarrow x\in\left\{-2;-4;0;-6;6;-12\right\}\)
Vậy \(x\in\left\{-2;-4;0;\pm6;-12\right\}\).
Bài 2:
a) Để \(\dfrac{n+5}{n-2}\in Z\)
thì \(n+5⋮n-2\)
\(\Rightarrow\left(n-2\right)+7⋮n-2\)
mà \(n-2⋮n-2\Rightarrow7⋮n-2\)
\(\Rightarrow n-2\inƯ\left(7\right)\)
\(\Rightarrow n-2\in\left\{\pm1;\pm7\right\}\)
...
b) Tương tự bài a.

\(4)\)
\(\dfrac{-\left(-x\right)}{5}-\dfrac{2}{10}=\dfrac{1}{-5}-\dfrac{7}{50}\)
\(\Leftrightarrow\dfrac{x}{5}-\dfrac{2}{10}=\dfrac{1}{-5}-\dfrac{7}{50}\)
\(\dfrac{2x}{10}-\dfrac{2}{10}=\dfrac{-10}{50}-\dfrac{7}{50}\)
\(\Leftrightarrow\dfrac{2x-2}{10}=\dfrac{-10-7}{50}\)
\(\dfrac{2x-2}{10}=\dfrac{-17}{50}\)
\(\Leftrightarrow50\left(2x-2\right)=-17.10\)
\(100x-100=-170\)
\(100x=-170+100=-70\)
\(x=-70:100=\dfrac{-7}{10}\)
\(\dfrac{x+1}{5}=\dfrac{7}{x-1}\)
\(\left(x+1\right)\left(x-1\right)5.7\)
\(x\left(x-1\right)+1\left(x-1\right)=35\)
\(x^2-x+x-1=35\)
\(x^2-1=35\)
\(x^2=36\)
\(\Leftrightarrow x=\left\{\pm6\right\}\)
bạn có thể giải đc các bài còn lại k ? K phải mk ép bạn đâu nhưng nếu bạn lm đc thì giúp mk nha

1: \(\Leftrightarrow\left(\dfrac{2}{5}x+2\right)=-\dfrac{3}{2}\cdot\left(-4\right)=6\)
=>2/5x=4
hay x=10
2: \(x\left(x+1\right)=0\)
=>x=0 hoặc x+1=0
=>x=0 hoặc x=-1
3: \(2x-16=x+40\)
=>2x-x=40+16
=>x=56
4: \(\dfrac{x}{4}=\dfrac{9}{x}\)
nên \(x^2=36\)
=>x=6 hoặc x=-6

a) 32 . 3n = 35
=> 3n = 35 : 32
=> 3n = 33
=> n = 3
b) (22 : 4) . 2n = 4
=> (4 : 4) . 2n = 4
=> 2n = 4
=> 2n = 22
=> n = 2
c) \(\frac{1}{9}.3^4.3^n=3^7\)
\(\Rightarrow3^{-2}.3^4.3^n=3^7\)
\(\Rightarrow3^{-2+4+n}=3^7\)
\(\Rightarrow3^{2+n}=3^7\)
\(\Rightarrow2+n=7\)
\(\Rightarrow n=5\)
d) \(\frac{1}{9}.27^n=3^n\)
\(\Rightarrow3^{-2}.3^{3n}=n\)
\(\Rightarrow3^{-2+3n}=n\)
\(\Rightarrow-2+3n=n\)
\(\Rightarrow2n=2\)
\(\Rightarrow n=1\)

Bài 1
2.|x+1|-3=5
2.|x+1| =8
|x+1| =4
=>x+1=4 hoặc x+1=-4
<=>x= 3 hoặc -5
Bài 3
A=2/n-1
Để A có giá trị nguyên thì n là
2 phải chia hết cho n-1
U(2)={1,2,-1,-2}
Vậy A là số nguyên khi n=2;3;0;-1
k mk nha. Chúc bạn học giỏi
Thank you
bài 1 :
\(2\cdot|x+1|-3=5\)
\(2\cdot|x+1|=5+3\)
\(2\cdot|x+1|=8\)
\(|x+1|=8\div2\)
\(|x+1|=4\)
\(x=4-3\)
\(x=3\Rightarrow|x|=3\)
bài 2 : có 2 trường hợp để \(n\in Z\)là \(A=2\)và \(A=4\)
TH1:
\(2=\frac{n+1}{n-2}\Rightarrow2=\frac{6}{3}\left(n\in Z\right)\)
\(2=\frac{n+1}{n-2}\Rightarrow2=\frac{6-1}{3+2}=5\)
\(\Rightarrow n=5\)
TH2
\(4=\frac{n+1}{n-2}\Rightarrow4=\frac{4}{1}\left(n\in Z\right)\)
\(\Rightarrow4=\frac{4-1}{1+2}=3\)
\(\Rightarrow n=3\)
\(n\in\left\{5;3\right\}\left(n\in Z\right)\)
Bài 3 có 2 trường hợp là \(A=1\)và \(A=2\)
TH1:
\(1=\frac{2}{n-1}\Rightarrow1=\frac{2}{2}\)
\(1=\frac{2}{2+1}=3\)
\(\Rightarrow n=3\)
TH2 :
\(2=\frac{2}{n-1}\Rightarrow2=\frac{2}{1}\)
\(2=\frac{2}{1+1}=2\)
\(\Rightarrow n=2\)
vậy \(\Rightarrow n\in\left\{3;2\right\}\)

a) (2n-1)4 : (2n-1) = 27
(2n-1)3 = 27 =33
=> 2n - 1= 3
=> 2n = 4
n = 2
phần b,c làm tương tự nha bn
d) (21+n) : 9 = 95:94
(2n+1) : 9 = 9
2n + 1 = 81
2n = 80
n = 40

2, ta thấy:
\(\dfrac{2008}{2009}< \dfrac{2008}{2009+2010}\left(1\right)\)
\(\dfrac{2009}{2010}< \dfrac{2009}{2009+20010}\left(2\right)\)
từ (1) và (2) cộng vế với vế ta đc :\(\dfrac{2008}{2009}+\dfrac{2009}{20010}< \dfrac{2008}{2009+2010}+\dfrac{2009}{2009+2010}=\dfrac{2008+2009}{2009+2010}\)

Bài 1 :
Sửa đề :
Tìm \(n\in Z\) để những phân số sau đồng thời có giá trị nguyên
\(\dfrac{-12n}{n};\dfrac{15}{n-2};\dfrac{8}{n+1}\)
Làm
Ta có :
\(\dfrac{-12n}{n}=-12\)
\(\Leftrightarrow\) Với mọi \(n\) thì \(\dfrac{-12n}{n}\) đều có giá trị nguyên \(\left(1\right)\)
Để \(\dfrac{15}{n-2}\in Z\) \(\Leftrightarrow n-2\inƯ\left(15\right)=\left\{\pm1;\pm15;\pm3;\pm5\right\}\)
\(\Leftrightarrow n\in\left\{-13;\pm3;\pm1;5;7;17\right\}\left(1\right)\)
Để \(\dfrac{8}{n+1}\in Z\Leftrightarrow n+1\inƯ\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
\(\Leftrightarrow n\in\left\{-9;-5;\pm3;-2;0;1;7\right\}\left(3\right)\)
Từ \(\left(1\right)+\left(2\right)+\left(3\right)\Leftrightarrow n\in\left\{\pm3;1;7\right\}\)

BÀi 1
Để A \(\in\) Z
=>\(\left(n+2\right)⋮\left(n-5\right)\)
=>\([\left(n-5\right)+7]⋮\left(n-5\right)\)
=>\(7⋮\left(n-5\right)\)
=>\(n-5\in\left\{1;7;-1;-7\right\}\)
=>\(n\in\left\{6;13;4;-2\right\}\)
Vậy \(n\in\left\{6;13;4;-2\right\}\)