
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Rút y ở phương trình thứ nhất, rồi thay vào phương trình thứ hai để tìm x.
Từ phương trình thứ nhất ta có:
\(y=13+4x\)(*)
Thay y vào phương trình thứ hai ta có:
\(-4+2\left(13+4x\right)=22\)
Từ đó tự tính: Nếu mày đã học nghiệm rồi
\(x=-1\)
Thay x vào (*) ta tìm y:
\(y=13+4.\left(-1\right)\)
Vậy hiệu nghiệm của hệ phương trình này là:
\(\hept{\begin{cases}x=-1\\y=9\end{cases}}\)
Ta có :
\(\hept{\begin{cases}4x-y=13\\-4x+2y=22\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}4x=13+y\\-\left(13+y\right)+2y=22\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}4x=13+y\\-13-y+2y=22\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}4x=13+y\\-13+y=22\end{cases}}\Leftrightarrow\hept{\begin{cases}4x=13+y\\y=35\end{cases}\Leftrightarrow\hept{\begin{cases}4x=13+35\\y=35\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}4x=48\\y=35\end{cases}\Leftrightarrow\hept{\begin{cases}x=12\\y=35\end{cases}}}\)

\(1,3x+2y=7\\ \Leftrightarrow2y=7-3x\left(1\right)\)
Vì \(2y⋮2\)
\(\Leftrightarrow3x-7⋮2\\ \Leftrightarrow3x-9⋮2\\ \Leftrightarrow3\left(x-3\right)⋮2\\ \Leftrightarrow x-3⋮2\\ \Leftrightarrow x.lẻ\)
Đặt \(x=2k+1\left(k\in Z\right)\)
Thay vào (1), ta được :
\(\left(1\right)\Leftrightarrow2y=3\left(2k+1\right)-7\\ \Leftrightarrow2y=6k+3-7\\ \Leftrightarrow2y=6k-4\\ \Leftrightarrow y=3k-2\)
Vậy \(x=2k+1;y=3k-2\left(k\in Z\right)\)
\(2,C_1:\left\{{}\begin{matrix}-2x+y=1\\4x+5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x+2y=2\\4x+5y=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}4x+5y=2\\7y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{7}\\y=\dfrac{5}{7}\end{matrix}\right.\\ C_2:\left\{{}\begin{matrix}-2x+y=1\\4x+5y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1+2x\\4x+5y=3\end{matrix}\right.\Leftrightarrow4x+5+10x=3\\ \Leftrightarrow x=-\dfrac{1}{7}\Leftrightarrow y=1-\dfrac{2}{7}=\dfrac{5}{7}\)

Bài 1:
$x^2y+4y=x+6$
$\Leftrightarrow y(x^2+4)=x+6$
$\Leftrightarrow y=\frac{x+6}{x^2+4}$
Để $y$ nguyên thì $\frac{x+6}{x^2+4}$ nguyên
$\Rightarrow x+6\vdots x^2+4(1)$
$\Rightarrow x^2+6x\vdots x^2+4$
$\Rightarrow (x^2+4)+(6x-4)\vdots x^2+4$
$\RIghtarrow 6x-4\vdots x^2+4(2)$
Từ $(1); (2)\Rightarrow 6(x+6)-(6x-4)\vdots x^2+4$
$\Rightarrow 40\vdots x^2+4$
$\Rightarrow x^2+4\in\left\{4; 5; 8; 10; 20;40\right\}$ (do $x^2+4$ là số nguyên $\geq 4$)
$\Rightarrow x\in\left\{0; \pm 1; \pm 2; \pm 4; \pm 6\right\}$
Đến đây thay vào tìm $y$ thôi.
Bài 2:
Lấy PT(1) trừ PT (2) theo vế thu được:
$3x=5y-2$
$\Leftrightarrow x=\frac{5y-2}{3}$
Thay vào PT(1) thì:
$(2.\frac{5y-2}{3}+1)(y+2)=9$
$\Leftrightarrow 10y^2+19y-29=0$
$\Leftrightarrow (y-1)(10y+29)=0$
$\Rightarrow y=1$ hoặc $y=\frac{-29}{10}$
Với $y=1\Rightarrow x=\frac{5y-2}{3}=1$
Với $y=\frac{-29}{10}\Rightarrow x=\frac{5y-2}{3}=\frac{-11}{2}$

Nghiệm là:
\(\hept{\begin{cases}x=6\\y=2\end{cases}}\)thảo mãn
P/s: Mk ko chắc đâu nhé
Rút x ở phương trình thứ hai, rồi thay vào phương trình thứ nhất để tìm y.
Từ phương trình thứ hai ta có:
\(x=-3+4y\) ( * )
Thay x vào phương trình thứ nhất ta có:
\(4\left(-3+4y\right)-5y=-12\)
Giải ra ta được
\(y=0\)
Thay y vào (*) ta tìm x:
\(x=-3+4.0\)
\(x=-3\)
Vậy nghiệm của hệ phương trình là:
\(\hept{\begin{cases}x=-3\\y=0\end{cases}}\)

Ta có: \(\left(x+2y\right)\left(3x+4y\right)=96\) ( x,y nguyên)
Lại có: \(3x+4y-\left(x+2y\right)=2x+2y\) ( chẵn)
=> 3x+4y , x+2y cùng chẵn hoặc cùng lẻ ( 1)
Mà (x+2y)(3x+4y)=96 chẵn
=> 3x+4y, x+2y cùng chẵn hoặc là một chẵn 1 lẻ ( 2)
Từ (1) và (2) => 3x+4y, x+2y cùng chẵn
Ta có bảng sau:
| 3x+4y | 48 | 2 | 24 | 4 | 16 | 6 | 12 | 8 |
| x+2y | 2 | 48 | 4 | 24 | 6 | 16 | 8 | 12 |
| x | 44 | -94 | 16 | -44 | 4 | -26 | -4 | -16 |
| y | -21 | 71 | -6 | 34 | 1 | 21 | 6 | 14 |
Vậy ...

Để hệ pt có nghiệm duy nhất khi \(3\ne\frac{2}{m}\Leftrightarrow3m\ne2\Leftrightarrow m\ne\frac{2}{3}\)
Với \(m\ne\frac{2}{3}\)hệ pt có nghiệm suy nhất
\(\hept{\begin{cases}3x+2y=m\\x+my=3\end{cases}\Leftrightarrow\hept{\begin{cases}3x+2y=m\\3x+3my=9\end{cases}\Leftrightarrow\hept{\begin{cases}\left(2-3m\right)y=m-9\\x+my=3\end{cases}}}}\)
\(\left(1\right)\Rightarrow y=\frac{m-9}{2-3m}\)
\(\left(2\right)\Rightarrow x=3-my=3-\frac{m^2-9m}{2-3m}=\frac{6-9m-m^2+9m}{2-3m}=\frac{6-m^2}{2-3m}\)
Thay vào biểu thức trên ta được :
\(\frac{18-3m^2}{2-3m}+\frac{4m-36}{2-3m}=-5\Rightarrow-18-3m^2+4m=-10+15m\)
\(\Leftrightarrow-3m^2-11m-8=0\Leftrightarrow\left(3m+8\right)\left(m+1\right)=0\Leftrightarrow m=-\frac{8}{3};m=-1\)( tmđk )
check lại hộ mình nhé =)

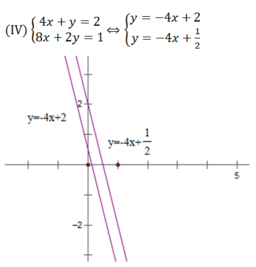
Hai đường thẳng trên song song nên chúng không có điểm chung hay hệ phương trình (IV) vô nghiệm.
Phương pháp thế:
Ta có ( biểu diễn y theo x từ phương trình thứ nhất):
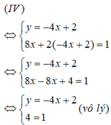
Vậy hệ phương trình (IV) vô nghiệm.

Ta có :
\(4x+4y=12\)
\(\Rightarrow x+y=3\)
\(\Rightarrow x=3-y\)
Mà \(x-2y=-21\)
\(\Rightarrow3-y-2y=-21\)
\(\Rightarrow-3y=-24\)
\(\Leftrightarrow y=8\)
\(\Rightarrow4x+8.4=12\)
\(\Rightarrow4x=12-32\)
\(\Rightarrow4x=-20\)
\(\Rightarrow x=-5\)
KL \(\orbr{\begin{cases}x=-5\\y=8\end{cases}}\)
có
x-2y=-21 và 4x+4y=12
<=> x-2y=-21 và x+y=3
trừ 2 vế , ta được
-3y=-24 và x=3-y
<=> y=8 và x = 3-8=-5
vậy x=-5 và y=8