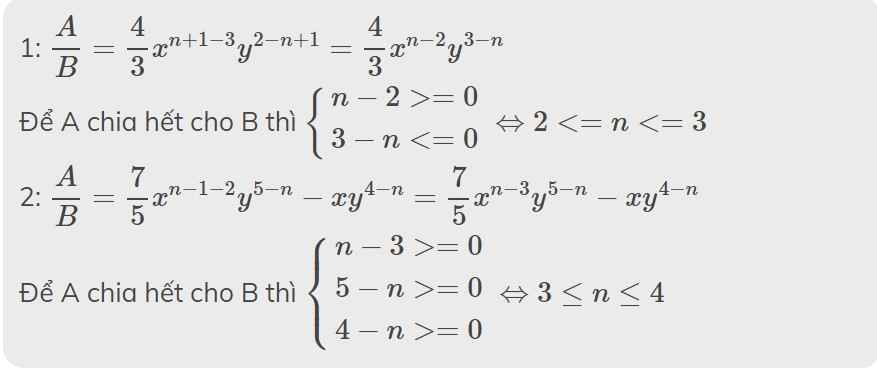a: \(7x^{n-3}:\left(-8x^5\right)=-\dfrac{7}{8}x^{n-3-5}=-\dfrac{7}{8}x^{n-8}\)

Để đây là phép chia hết thì n-8>=0

hay n>=8

b: \(\dfrac{\left(3x^{n+1}-2x^5\right)}{-5x^3}=-\dfrac{3}{5}x^{n+1-3}+\dfrac{2}{5}x^2=\dfrac{-3}{5}x^{n-2}+\dfrac{2}{5}x^2\)

Để đây là phép chia hết thì n-2>=0

hay n>=2

a,Để phép chia thực hiện đc<=>x^n<=x^5=>n<=5=>n=(0;1;2;3;4;5)

                                                    y^n<=y=>n<=1=>n=(1;0)

Từ hai ý trên=>n=(0;1)

b,,Để phép chia thực hiện đc<=>x^n+1<=x^2=>n+1<=2=>n=(0;1)

                                                    y^n=1<=y^2=>n+1<=2=>n=(0;1)

Từ hai ý trên =>n=(0;1)

1: \(\dfrac{A}{B}=\dfrac{4}{3}x^{n+1-3}y^{2-n+1}=\dfrac{4}{3}x^{n-2}y^{3-n}\)

Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-2>=0\\3-n< =0\end{matrix}\right.\Leftrightarrow2< =n< =3\)

2: \(\dfrac{A}{B}=\dfrac{7}{5}x^{n-1-2}y^{5-n}-xy^{4-n}=\dfrac{7}{5}x^{n-3}y^{5-n}-xy^{4-n}\)

Để A chia hết cho B thì \(\left\{{}\begin{matrix}n-3>=0\\5-n>=0\\4-n>=0\end{matrix}\right.\Leftrightarrow3\le n\le4\)

a) \(\left(4x-1\right)^2-\left(3x+2\right)\left(3x-2\right)=\left(7x-1\right)\left(x+2\right)+\left(2x+1\right)^2-\left(4x^2+7\right)\)(1)

\(\Leftrightarrow\left(16x^2-8x+1\right)-\left(9x^2-4\right)=\left(7x^2+14x-x-2\right)+\left(4x^2+4x+1\right)-\left(4x^2+7\right)\)

\(\Leftrightarrow16x^2-8x+1-9x^2+4=7x^2+13x-2+4x^2+4x+1-4x^2-7\)

\(\Leftrightarrow7x^2-8x+5=7x^2+17x-8\)

\(\Leftrightarrow7x^2-8x-7x^2-17x=-8-5\)

\(\Leftrightarrow-25x=-13\)

\(\Leftrightarrow x=\dfrac{13}{25}\)

Vậy tập nghiệm phương trình (1) là \(S=\left\{\dfrac{13}{25}\right\}\)

gắp cái gì