Ta có:

\(\dfrac{x}{2}=\dfrac{y}{3}=k\)

Theo đề bài, ta có :

\(xy=54\Rightarrow2k.3k=54\)

\(\Rightarrow5k=54\Rightarrow k=10,8\)

Ta thấy :

\(\dfrac{x}{2}=10,8\Rightarrow x=10,8.2=21,6\)

\(\dfrac{y}{3}=10,8\Rightarrow y=10,8.3=32,4\)

Đặt :\(\dfrac{x}{2}=\dfrac{y}{3}=k\Leftrightarrow\left\{{}\begin{matrix}x=2k\\y=3k\end{matrix}\right.\)

mà \(xy=54\)

hay 2k . 3k = 54

\(\Rightarrow6.k^2=54\)

\(\Rightarrow k^2=9=\left(\pm3\right)^2\)

Với k = 3 \(\Rightarrow\) \(x=2.3=6;y=3.3=9\)

Với k = -3 \(\Rightarrow x=2.\left(-3\right)=-6;y=3.\left(-3\right)=-9\)

1. Áp dụng tc dãy TSBN, ta có:

\(\dfrac{x}{6}=\dfrac{y}{5}=\dfrac{z}{3}=\dfrac{x+y-z}{6+5-3}=\dfrac{54}{8}=\dfrac{27}{4}\)

+\(\dfrac{x}{6}=\dfrac{27}{4}\Rightarrow x=\dfrac{27.6}{4}=\dfrac{81}{2}\)

+\(\dfrac{y}{5}=\dfrac{27}{4}\Rightarrow y=\dfrac{27.5}{4}=\dfrac{135}{4}\)

+\(\dfrac{z}{3}=\dfrac{27}{4}\Rightarrow z=\dfrac{27.3}{4}=\dfrac{81}{4}\)

Vậy \(x=\dfrac{81}{2};y=\dfrac{135}{4};z=\dfrac{81}{4}\)

2,Áp dụng tc dãy TSBN, ta có:

\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{c}{4}=\dfrac{x+2y-3c}{2+2.3+3.4}=\dfrac{-20}{20}=-1\)

+\(\dfrac{x}{2}=-1\Rightarrow x=-1.2=-2\)

+\(\dfrac{y}{3}=-1\Rightarrow y=-1.3=-3\)

+\(\dfrac{c}{4}=-1\Rightarrow c=-1.4=-4\)

Vậy \(x=-2;y=-3;c=-4\)

xy = 96 => x = 96/y => 2/x = y/48

=> y/48 = 3/y => y = 12 hoặc -12

=> x = 8 hoặc -8

\(\dfrac{2}{x}=\dfrac{3}{y}\) và x.y =96

\(=>\dfrac{x}{2}=\dfrac{y}{3}=k\)

=> x = 2k và y = 3k

Thay vào x.y = 96

(2k . 3k) = 96

\(6k^2=96\)

\(k^2=96:6\)

\(k^2=16\)

\(k=-4\) hoặc \(+4\)

Với k = - 4 => x = 2 . ( - 4 ) = - 8

y = 3 . ( - 4) = - 12

Với k = 4 => x = 2 . 4 = 8

y = 3 . 4 = 12

\(=\dfrac{2}{x}-\left(\dfrac{x^2}{x\left(x+y\right)}-\dfrac{x^2-y^2}{xy}-\dfrac{y^2}{y\left(x+y\right)}\right):\dfrac{x^3-y^3}{x^2-y^2}\)

\(=\dfrac{2}{x}-\left(\dfrac{x^2y-\left(x^2-y^2\right)\left(x+y\right)-y^2x}{xy\left(x+y\right)}\right)\cdot\dfrac{x+y}{x^2+xy+y^2}\)

\(=\dfrac{2}{x}-\dfrac{x^2y-x^3-x^2y+xy^2+y^3-xy^2}{xy}\cdot\dfrac{1}{x^2+xy+y^2}\)

\(=\dfrac{2}{x}-\dfrac{-\left(x-y\right)\left(x^2+xy+y^2\right)}{xy}\cdot\dfrac{1}{x^2+xy+y^2}\)

\(=\dfrac{2}{x}+\dfrac{x-y}{xy}=\dfrac{y+x-y}{xy}=\dfrac{1}{y}\)

Câu 1 :

a. Theo đề bài ta có :

\(\dfrac{x}{2}=\dfrac{y}{5}\) và \(x+y=21\)

Áp dụng t/c dãy tỉ số bằng nhau :

\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{21}{7}=3\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{2}=3\Rightarrow x=2.3=6\\\dfrac{y}{5}=3\Rightarrow y=3.5=15\end{matrix}\right.\)

Vậy..............

b. Đặt \(\dfrac{x}{2}=\dfrac{y}{3}=k\Leftrightarrow\left\{{}\begin{matrix}2k\\3y\end{matrix}\right.\)

mà \(x.y=54\)

hay \(2k.3k=54\)

\(\Rightarrow6.k^2=54\)

\(\Rightarrow k^2=9=\left(\pm3\right)^2\)

Với \(k=3\Rightarrow\left\{{}\begin{matrix}x=2.3=6\\y=3.3=9\end{matrix}\right.\)

Với \(k=-3\Rightarrow\left\{{}\begin{matrix}x=\left(-3\right).2=-6\\y=\left(-3\right).3=-9\end{matrix}\right.\)

Vậy..............

c. Áp dụng t/c dãy tỉ số bằng nhau ta có :

\(\dfrac{x}{7}=\dfrac{y}{5}=\dfrac{x-y}{7-5}=\dfrac{12}{2}=6\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{7}=6\Rightarrow x=7.6=42\\\dfrac{y}{5}=6\Rightarrow y=5.6=40\end{matrix}\right.\)

Vậy............

Nhờ các bạn trả lời giúp mik

1/ a, Ta có :

\(x-2y+3z=35\)

\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)

\(\Leftrightarrow\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{x}{3}=\dfrac{2y}{8}=\dfrac{3z}{15}=\dfrac{x-2y+3z}{3-8+15}=\dfrac{35}{10}=\dfrac{7}{2}\)

\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}=\dfrac{7}{2}\Leftrightarrow x=\dfrac{21}{2}\\\dfrac{x}{4}=\dfrac{7}{2}\Leftrightarrow y=14\\\dfrac{z}{5}=\dfrac{7}{2}\Leftrightarrow z=\dfrac{35}{2}\end{matrix}\right.\)

Vậy ..

Đặt k = . Ta có x = 2k, y = 5k

Từ xy=10. suy ra 2k.5k = 10 => 10 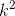= 10 => 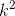= 1 => k = ± 1

Với k = 1 ta được = 1 suy ra x = 2, y = 5

Với k = -1 ta được = -1 suy ra x = -2, y = -5

Gọi \(\dfrac{x}{2}=\dfrac{y}{5}=k\)

Với \(\dfrac{x}{2}=k\Rightarrow x=2k\); \(\dfrac{y}{5}=k\Rightarrow y=5k\)

Theo đề bài,ta còn có:

\(xy=10\)

hay 2k.5k=10

10k² =10

\(\Rightarrow k=\pm1\)

Với k=1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=1\Rightarrow x=2;y=5\)

Với k=-1 \(\Rightarrow\dfrac{x}{2}=\dfrac{y}{5}=-1\Rightarrow x=-2;y=-5\)

❏Ta có : \(\left\{{}\begin{matrix}\dfrac{x}{2}=\dfrac{y}{2}\\xy=54\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=y\\xy=54\end{matrix}\right.\)

\(\Rightarrow x^2=54\Rightarrow x=y=\sqrt{54}=3\sqrt{6}\)

Ta có : \(\left\{{}\begin{matrix}\frac{x}{2}=\frac{y}{2}\\xy=54\end{matrix}\right.=>\left\{{}\begin{matrix}x=y\\xy=54\end{matrix}\right.\)

⇒\(x^2=54\)=>x=y=\(\sqrt{54=3\sqrt{6}}\)

Theo đề bài ta có :

\(\dfrac{x-y}{3}=\dfrac{x+y}{13}\)

Áp dụng t/c dãy tỉ số bằng nhau ta có :

\(\dfrac{x-y}{3}=\dfrac{x+y}{13}=\dfrac{x-y+x+y}{3+13}=\dfrac{2x}{16}=\dfrac{x}{8}\)

\(\dfrac{x}{8}=\dfrac{xy}{200}\Leftrightarrow\) \(\dfrac{x}{xy}=\dfrac{8}{200}\Rightarrow\) \(\dfrac{1}{y}=\dfrac{1}{25}\) \(\Rightarrow y=25\)

Thay y = 25 vào biểu thức ta có :

\(\dfrac{x-25}{3}=\dfrac{x+25}{13}\)

\(\Leftrightarrow\) \(13x-325=3x+75\)

\(\Leftrightarrow13x-3x=75+325\)

\(\Leftrightarrow10x=400\)

\(\Rightarrow x=40\)

Vậy \(x=40\) ; \(y=25\)

Mơn ạk <3