Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(B=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\)
\(\Rightarrow B=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}\)
\(\Rightarrow B=\dfrac{3}{2.3}-\dfrac{2}{2.3}+\dfrac{4}{3.4}-\dfrac{3}{3.4}+...+\dfrac{10}{9.10}-\dfrac{9}{9.10}\)
\(\Rightarrow B=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
\(\Rightarrow B=\dfrac{1}{2}-\dfrac{1}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)
\(B=\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\\ B=\dfrac{1}{2.3}+\dfrac{1}{3.4}+\dfrac{1}{4.5}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}\\ B=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}\\ B=\dfrac{1}{2}-\dfrac{1}{10}\\ B=\dfrac{5}{10}-\dfrac{1}{10}\\ B=\dfrac{4}{10}\\ B=\dfrac{2}{5}\)

1,A=\(\dfrac{1}{2.3}\)+\(\dfrac{1}{3.4}\)+\(\dfrac{1}{4.5}\)+...+\(\dfrac{1}{99.100}\)
1,A= \(\dfrac{1}{2}\)-\(\dfrac{1}{3}\)+\(\dfrac{1}{3}\)-\(\dfrac{1}{4}\)+\(\dfrac{1}{4}\)-\(\dfrac{1}{5}\)+\(\dfrac{1}{5}\)-...-\(\dfrac{1}{99}\)+\(\dfrac{1}{99}\)-\(\dfrac{1}{100}\)
1,A= \(\dfrac{1}{2}\)-\(\dfrac{1}{100}\)
1,A= \(\dfrac{49}{100}\)
(Còn câu 2 mình chưa nghĩ ra. Cho mình hỏi 1 câu, không biết là đề câu 2 có chính xác không?)
đề này do cô giáo lớp mình cho mình cũng đc chữa câu 1 rồi còn câu 2 thì tiếp tục nghĩ

Bài 1: Ta có:
\(M=\dfrac{20}{112}+\dfrac{20}{280}+\dfrac{20}{520}+\dfrac{20}{832}\)
\(=\dfrac{20}{8.14}+\dfrac{20}{14.20}+\dfrac{20}{20.26}+\dfrac{20}{26.32}\)
\(=\dfrac{20}{6}\left(\dfrac{6}{8.14}+\dfrac{6}{14.20}+\dfrac{6}{20.26}+\dfrac{6}{26.32}\right)\)
\(=\dfrac{20}{6}\left(\dfrac{1}{8}-\dfrac{1}{14}+\dfrac{1}{14}-\dfrac{1}{20}+...+\dfrac{1}{26}-\dfrac{1}{32}\right)\)
\(=\dfrac{20}{6}\left(\dfrac{1}{8}-\dfrac{1}{32}\right)=\dfrac{20}{6}.\dfrac{3}{32}=\dfrac{5}{16}\)
Vậy \(M=\dfrac{5}{16}\)
Bài 2: Ta có:
\(A=\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+...+\dfrac{1}{210}\)
\(=\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}+...+\dfrac{1}{14.15}\)
\(=\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+...+\dfrac{1}{14}-\dfrac{1}{15}\)
\(=\dfrac{1}{6}-\dfrac{1}{15}=\dfrac{1}{10}\)
Vậy \(A=\dfrac{1}{10}\)
Giải:
\(M=\dfrac{20}{112}+\dfrac{20}{280}+\dfrac{20}{520}+\dfrac{20}{832}.\)
\(M=\dfrac{5}{28}+\dfrac{5}{70}+\dfrac{5}{130}+\dfrac{5}{208}.\)
\(M=\dfrac{5}{4.7}+\dfrac{5}{7.10}+\dfrac{5}{10.13}+\dfrac{5}{13.16}.\)
\(M=\dfrac{5}{3}\left(\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{16}\right).\)
\(M=\dfrac{5}{3}\left[\left(\dfrac{1}{7}-\dfrac{1}{7}\right)+\left(\dfrac{1}{10}-\dfrac{1}{10}\right)+\left(\dfrac{1}{13}-\dfrac{1}{13}\right)+\left(\dfrac{1}{4}-\dfrac{1}{16}\right)\right].\)
\(M=\dfrac{5}{3}\left[0+0+0+\left(\dfrac{1}{4}-\dfrac{1}{16}\right).\right]\)
\(M=\dfrac{5}{3}\left(\dfrac{1}{4}-\dfrac{1}{16}\right).\)
\(M=\dfrac{5}{3}\left(\dfrac{4}{16}-\dfrac{1}{16}\right).\)
\(M=\dfrac{5}{3}.\dfrac{3}{16}.\)
\(M=\dfrac{15}{48}=\dfrac{5}{16}.\)

\(S=\dfrac{1}{2}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}\)
\(S=\dfrac{1}{2}+\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}+\dfrac{1}{10.11}\)
\(S=\dfrac{1}{2}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}\)\(S=\dfrac{1}{2}+\dfrac{1}{5}-\dfrac{1}{11}\)
\(S=\dfrac{67}{110}\)

\(A=\dfrac{1}{2}.\dfrac{1}{3}+\dfrac{1}{3}.\dfrac{1}{4}+...+\dfrac{1}{8}.\dfrac{1}{9}\)
\(=\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{8.9}\)
\(=\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{8}-\dfrac{1}{9}\)
\(=\dfrac{1}{2}-\dfrac{1}{9}\)
\(=\dfrac{7}{18}\)
\(B=\dfrac{1}{20}+\dfrac{1}{30}+...+\dfrac{1}{110}\)
\(=\dfrac{1}{4.5}+\dfrac{1}{5.6}+...+\dfrac{1}{10.11}\)
\(=\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{10}-\dfrac{1}{11}\)
\(=\dfrac{1}{4}-\dfrac{1}{11}\)
\(=\dfrac{7}{44}\)

E=\(\dfrac{1}{90}-\dfrac{1}{72}-\dfrac{1}{56}-\dfrac{1}{42}-\dfrac{1}{30}-\dfrac{1}{20}-\dfrac{1}{12}-\dfrac{1}{6}-\dfrac{1}{2}\\ E=\dfrac{1}{90}-\left(\dfrac{1}{72}+\dfrac{1}{56}+\dfrac{1}{42}+\dfrac{1}{30}+\dfrac{1}{20}+\dfrac{1}{12}+\dfrac{1}{6}+\dfrac{1}{2}\right)\\ E=\dfrac{1}{90}-\left(\dfrac{1}{9.8}+\dfrac{1}{8.7}+\dfrac{1}{7.6}+\dfrac{1}{6.5}+\dfrac{1}{5.4}+\dfrac{1}{4.3}+\dfrac{1}{3.2}+\dfrac{1}{2.1}\right)\\ E=\dfrac{1}{90}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}\right)\\ E=\dfrac{1}{90}-\left(1-\dfrac{1}{9}\right)\\ E=\dfrac{1}{90}-\dfrac{8}{9}\\ E=\dfrac{1}{90}-\dfrac{80}{90}\\ E=-\dfrac{79}{90}\)Vậy:\(E=-\dfrac{79}{90}\)
E=\(\dfrac{1}{10.9}-\dfrac{1}{9.8}-\dfrac{1}{8.7}-\dfrac{1}{7.6}-\dfrac{1}{6.5}-\dfrac{1}{5.4}-\dfrac{1}{4.3}-\dfrac{1}{3.2}-\dfrac{1}{2.1}\)
E=\(\dfrac{1}{10}-\dfrac{1}{1}\)
E=\(\dfrac{-9}{10}\)

\(A=\dfrac{-1}{20}+\dfrac{-1}{30}+\dfrac{-1}{42}+\dfrac{-1}{56}+\dfrac{-1}{72}+\dfrac{-1}{90}\)
\(=-\left(\dfrac{1}{20}+\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}\right)\)
\(=-\left(\dfrac{1}{4\cdot5}+\dfrac{1}{5\cdot6}+\dfrac{1}{6\cdot7}+\dfrac{1}{7\cdot8}+\dfrac{1}{8\cdot9}+\dfrac{1}{9\cdot10}\right)\)
\(=-\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{9}-\dfrac{1}{10}\right)\)
\(=-\left(\dfrac{1}{4}-\dfrac{1}{10}\right)\)\(=-\dfrac{3}{20}\)
Bài 1. ko quy đồng hãy tính hợp lý:
\(A=\dfrac{-1}{20}+\dfrac{-1}{30}+\dfrac{-1}{42}+\dfrac{-1}{56}+\dfrac{-1}{72}+\dfrac{-1}{90}\)
\(A=\dfrac{-1}{4.5}+\dfrac{-1}{5.6}+\dfrac{-1}{6.7}+\dfrac{-1}{7.8}+\dfrac{-1}{8.9}+\dfrac{-1}{9.10}\)
\(A=\dfrac{-1}{4}-\dfrac{-1}{5}+\dfrac{-1}{5}-\dfrac{-1}{6}+\dfrac{-1}{6}-\dfrac{-1}{7}+\dfrac{-1}{7}-\dfrac{-1}{8}+\dfrac{-1}{8}-\dfrac{-1}{9}+\dfrac{-1}{9}-\dfrac{-1}{10}\)
\(A=\dfrac{-1}{4}-\dfrac{-1}{10}\)
\(A=\dfrac{-3}{20}\)

D = 1 + \(\dfrac{-1}{20}\) + \(\dfrac{-1}{30}\) + \(\dfrac{-1}{42}\)+ \(\dfrac{-1}{56}\)+ \(\dfrac{-1}{72}\)+ \(\dfrac{-1}{90}\)
D = 1 - ( \(\dfrac{1}{4\times5}\) + \(\dfrac{1}{5\times6}\)+ \(\dfrac{1}{6\times7}\)+ \(\dfrac{1}{7\times8}\)+\(\dfrac{1}{8\times9}\)+\(\dfrac{1}{9\times10}\))
D = 1 - ( \(\dfrac{1}{4}\) - \(\dfrac{1}{10}\))
D = 1 - \(\dfrac{3}{20}\)
D = \(\dfrac{17}{20}\)
D=1+(1/4x5+1/5x6+1/6x7+1/7x8+1/8x9+1/9x10)
D=1+(1/4-1/5+1/5-1/6+1/6-1/7+1/7-1/8+1/8-1/9+1/9-1/10)
D=1+(1/4-1/10)
D=1+3/5
D=8/5
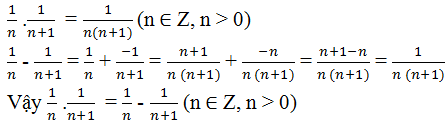

\(A=\dfrac{1}{30}+\dfrac{1}{42}+\dfrac{1}{56}+\dfrac{1}{72}+\dfrac{1}{90}+\dfrac{1}{110}+\dfrac{1}{132}\)
\(=\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}+\dfrac{1}{10.11}+\dfrac{1}{11.12}\)
\(=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{12}\)
\(=\dfrac{1}{5}-\dfrac{1}{12}=\dfrac{12}{60}-\dfrac{5}{60}=\dfrac{7}{60}\)
Vậy \(A=\dfrac{7}{60}\)
\(A=\dfrac{1}{5.6}+\dfrac{1}{6.7}+\dfrac{1}{7.8}+\dfrac{1}{8.9}+\dfrac{1}{9.10}+\dfrac{1}{10.11}+\dfrac{1}{11.12}\)
\(A=\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{10}+\dfrac{1}{10}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{12}\)
\(A=\dfrac{1}{5}-\dfrac{1}{12}\)
\(A=\dfrac{7}{60}\)